11.盛最多水的容器

算法

发布日期: 2023-09-13

更新日期: 2024-03-13

文章字数: 704

阅读时长: 3 分

问题

传送门：https://leetcode.cn/problems/container-with-most-water/

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

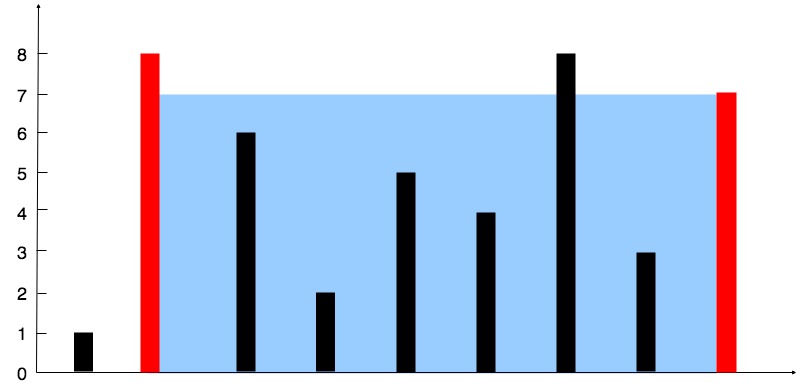
盛水最多的容器示意图

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

思路

要取到最大量的水，显然需要考虑两个因素：高度和垂线间隔。而高度就是两条垂线的较小值。因此我们设置双指针：头指针指向首部，尾指针指向尾部。那么如何移动指针呢？或者说，该移动哪一个指针？我们当然希望指针指向的垂线高度尽可能地高，因此我们将两个指针中所指向垂线高度较底者往右移动一位即可，这样才可能增大垂线高度。

比如上面的例子[1,8,6,2,5,4,8,3,7]中，头指针l=0，尾指针r=8，计算水量$V=\min\{ height[l],height[r] \}\times (r-l)=8$

此时$height[l]<height[r]$，因此右移头指针l=1，r=8，水量$V=\min\{ height[l],height[r] \}\times (r-l)=49$
此时$height[l]>height[r]$，因此左移尾指针r=7，l=1，水量$V=\min\{ height[l],height[r] \}\times (r-l)=18$
此时$height[l]>height[r]$，因此左移尾指针r=6，l=1，水量$V=\min\{ height[l],height[r] \}\times (r-l)=40$
此时$height[l]=height[r]$，不妨右移头指针l=2，r=6，水量$V=\min\{ height[l],height[r] \}\times (r-l)=24$
此时$height[l]<height[r]$，因此右移头指针l=3，r=6，水量$V=\min\{ height[l],height[r] \}\times (r-l)=6$
此时$height[l]<height[r]$，因此右移头指针l=4，r=6，水量$V=\min\{ height[l],height[r] \}\times (r-l)=10$
此时$height[l]<height[r]$，因此右移头指针l=5，r=6，水量$V=\min\{ height[l],height[r] \}\times (r-l)=4$
此时$height[l]<height[r]$，因此右移头指针l=6，r=6，两指针相遇，算法运行结束。

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size()-1;
        int ans = 0;
        while(i != j) {
            ans = max(ans, min(height[i], height[j]) * (j - i));
            if(height[i] < height[j])   i++;
            else    j--;
        }
        return ans;
    }
};