Boltzmann Machine，玻尔兹曼机

模型简介

玻尔兹曼机是一种基于能量的概率模型。常见的玻尔兹曼机有两层：显层和隐层，示意图如下。

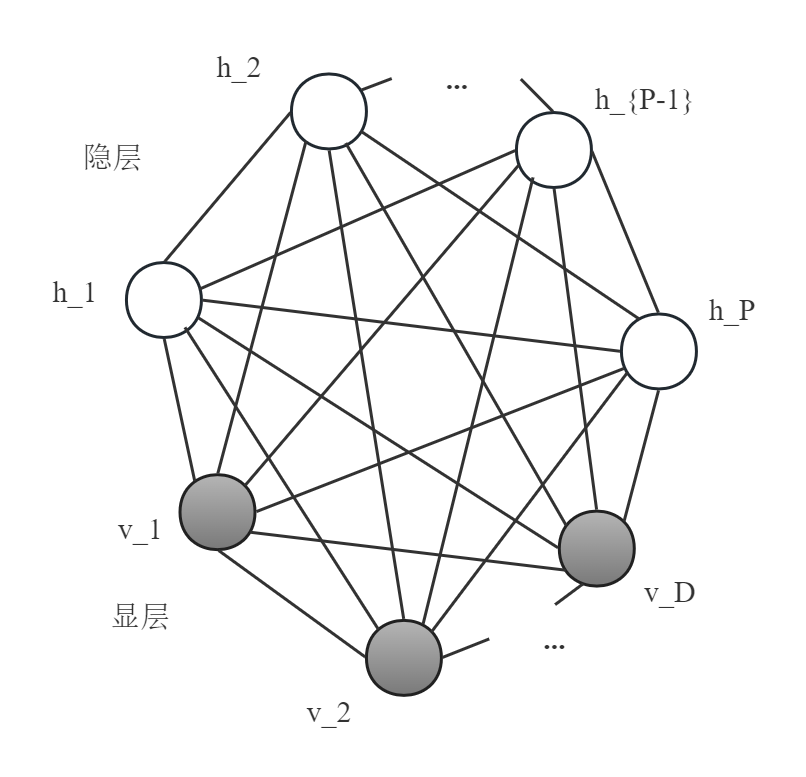
其中，显层$\mathbf{v}\in \{0,1\}^D$，隐层$\mathbf{h}\in\{0,1\}^P$。即显层有D个结点，隐层有P个结点，每一个结点的状态用0或者1表示，整体服从伯努利分布：

• $\mathbf{v}=[v_1,v_2,…,v_D]^T$
• $\mathbf{h}=[h_1,h_2,…,h_P]^T$

下面约定权重系数：

• $w_{ij}$表示连接显层结点$v_i$和隐层结点$h_j$的边权重
• $l_{ij}$表示连接两个显层结点$v_i$和$v_j$的边权重
• $j_{ij}$表示连接两个隐层结点$h_i$和$h_j$的边权重

基于能量定义玻尔兹曼机的概率密度函数

$$P(\mathbf{v},\mathbf{h})=\frac{e^{-E(\mathbf{v},\mathbf{h})}}{Z}$$

其中$Z$为配分函数

$$Z=\sum\limits_\mathbf{v}\sum\limits_\mathbf{h}e^{-E(\mathbf{v},\mathbf{h})}$$

其中$E(\mathbf{v},\mathbf{h})$即为模型的能量，定义为

$E(\mathbf{v},\mathbf{h})=-(\mathbf{v}^TW\mathbf{h}+\frac{1}{2}\mathbf{v}^TL\mathbf{v}+\frac{1}{2}\mathbf{h}^TJ\mathbf{h})$

上述公式上由三部分构成，可以看作隐层内部、显层内部和隐层显层之间的能量之和。不妨以隐层和显层之间进行分析：取任意两个结点$v_i,h_j$和之间的边$w_{ij}$，计算局部能量

$$\varepsilon_{ij}=v_iw_{ij}h_j$$

则这一部分的总的能量为

$$\sum\limits_{i=1}^D\sum\limits_{j=1}^P\varepsilon_{ij}=\sum\limits_{i=1}^D\sum\limits_{j=1}^Pv_iw_{ij}h_j=\mathbf{v}^TW\mathbf{h}\in \mathbb{R}$$

基于对数极大似然估计的梯度上升

这一部分，我们从极大似然估计出发，对概率密度$P(v,h)$进行极大值推导，其中

$$P(\mathbf{v},\mathbf{h})=\frac{e^{-E(\mathbf{v},\mathbf{h})}}{Z}$$

假设现在有样本集$V$，极大似然估计要求每一个样本出现的概率达到极大值，即边缘密度$\prod\limits_vP(v)$达到最大，其中

$$P(\mathbf{v})=\sum\limits_\mathbf{h}P(\mathbf{v},\mathbf{h})$$

由对数极大似然估计，将乘积进行转换

$$S=\log\prod\limits_\mathbf{v}P(\mathbf{v})=\sum\limits_\mathbf{v}\log P(\mathbf{v})$$

记参数$\theta=[W,J,L]$，它们的含义上文已经提过；只需求解

$$\frac{\partial S}{\partial \theta}=\sum\limits_\mathbf{v}\frac{\partial \log P(\mathbf{v})}{\partial \theta}$$

具体的数学推导见附录，这里直接给出结果

$$\begin{aligned} \frac{\partial S}{\partial \theta}&=\sum\limits_\mathbf{v}\frac{\partial \log P(\mathbf{v})}{\partial \theta}\\\\ &=\sum\limits_\mathbf{v}\sum\limits_\mathbf{h}P(\mathbf{v},\mathbf{h})\frac{\partial E(\mathbf{v},\mathbf{h})}{\partial \theta}-\sum\limits_\mathbf{h}P(\mathbf{h}|\mathbf{v})\frac{\partial E(\mathbf{v},\mathbf{h})}{\partial \theta} \end{aligned}$$

$\theta$由三个参数组成，我们以其中一个为例（$W$）进行说明

$$\begin{aligned} \frac{\partial S}{\partial W}&=\sum\limits_\mathbf{v}\sum\limits_\mathbf{h}P(\mathbf{v},\mathbf{h})\frac{\partial E(\mathbf{v},\mathbf{h})}{\partial W}-\sum\limits_\mathbf{h}P(\mathbf{h}|\mathbf{v})\frac{\partial E(\mathbf{v},\mathbf{h})}{\partial W}\\\\ &= \sum\limits_\mathbf{v}\sum\limits_\mathbf{h}P(\mathbf{h}|\mathbf{v})\mathbf{v}\mathbf{h}^T-|V|\sum\limits_\mathbf{v}\sum\limits_\mathbf{h}P(\mathbf{v},\mathbf{h})\mathbf{v}\mathbf{h}^T \end{aligned}$$

其中$P(h|v)$是真实数据的经验分布，记作$P_{data}$；而$P(v,h)$看作模型的后验分布，记作$P_{model}$。上式用期望表示为

$$\frac{\partial S}{\partial W}=\mathbb{E}_{p_{data}}(\mathbf{v}\mathbf{h}^T)-\mathbb{E}_{p_{model}}(\mathbf{v}\mathbf{h}^T)$$

同理有

$$\frac{\partial S}{\partial J}=\mathbb{E}_{p_{data}}(hh^T)-\mathbb{E}_{p_{model}}(hh^T)$$ $$\frac{\partial S}{\partial L}=\mathbb{E}_{p_{data}}(vv^T)-\mathbb{E}_{p_{model}}(vv^T)$$

因此，基于对数极大似然估计的梯度上升法，每一步的参数更新表示为

$$\begin{aligned} W\gets W+\eta \frac{\partial S}{\partial W} \\ J \gets J+\eta \frac{\partial S}{\partial J} \\ L \gets L+\eta \frac{\partial S}{\partial L} \end{aligned}$$

其中$\eta \in \mathbb{R}$指步长。

基于MCMC的梯度上升

我们已经建立了基于极大似然估计求出了梯度上升的数学模型。但是实际上对于普通的玻尔兹曼机（并非受限玻尔兹曼机），后验分布是无法求出的。基于MCMC的方法提供了一条解决思路，转化到受限玻尔兹曼机（简称RBM）中求解。

相比于普通的玻尔兹曼机，RBM有更多特性，都是基于它的网络结构是一个偶图。

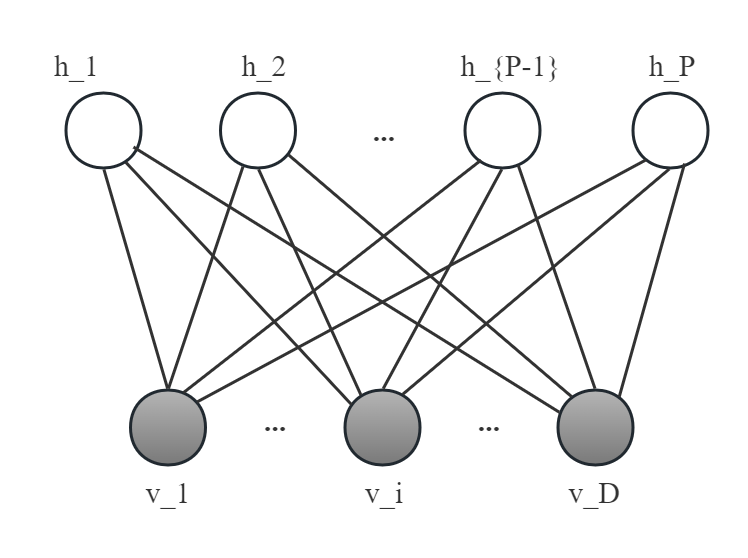
显层$v$，隐层$h$，我们约定

$$v_{-i}=\{ v_1,v_2,\dots, v_D \} - \{v_i\},\quad i\in \{1,2,\dots,D\}$$

在普通的玻尔兹曼机中有条件概率：

$$P(v_i=1|h,v_{-i})=\sigma(\sum\limits_{j=1}^PW_{ij}h_j+\sum\limits_{k=1,k\ne i}^DL_{ik}v_k) \\ P(h_j=1|v,h_{-j})=\sigma(\sum\limits_{i=1}^DW_{ij}v_i+\sum\limits_{k=1,k\ne j}^PJ_{jk}h_k)$$

在RBM中，由于显层内部、隐层内部不再有边相连，因此不同的隐层之间的状态互不相关，下式成立

$$P(h|v)=\prod\limits_{j=1}^PP(h_j|v)$$ $$P(h_j=1|v)=P(h_j=1|v,h_{-j})=\sigma(\sum\limits_{i=1}^DW_{ij}v_i)$$

平均场推断

虽然MCMC可以一定程度上解决上述问题，但是一旦采样规模变大，后验概率仍然无法求出。接下来从变分推断的平均场理论来求出后验概率。

赏