线性模型

给定$d$维样本点$\mathbf{x}=(x_1; x_2;…; x_d)$，线性模型要学习一个线性组合

$$f(\mathbf{x})=w_1x_1+w_2x_2+...+w_dx_d+b$$

用向量形式表示为

$$f(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b\quad w,x\in R^d$$

线性回归

当然，回归问题总是要学习一个“对象”，在线性回归中，这个“对象”就是上面的线性组合；为了评价学习到的结果到底怎么样，通常采用均方误差，来量化学习结果和真实值之间的差距

$$\mathrm{MSE}=\sum_{i=1}^m(f(\mathbf{x}^{(i)})-y^{(i)})^2$$

在此，约定$(\mathbf{x}^{(i)}, y^{(i)})$表示第i个数据样本，$x^{(i)}_j$表示第i个数据样本的第j个特征分量，$y^{(i)}$表示第i个样本的标签。

而根据数据集求解使得均方误差最小的模型参数$\mathbf{w},b$的过程，称为最小二乘参数估计。常用的方法是梯度下降，因此需要对参数求梯度

$$\begin{aligned} \frac{\partial MSE}{\partial \mathbf{w}}&=\frac{\partial\displaystyle \sum_{i=1}^m\left(\mathbf{w}^T\mathbf{x}^{(i)}+b-y^{(i)}\right)^2}{\partial \mathbf{w}}\\\\&=2\left(\mathbf{w}\sum_{i=1}^m(\mathbf{x}^{(i)})^2-\sum_{i=1}^m(y^{(i)}-b)\mathbf{x}^{(i)}\right) \end{aligned}$$

类似地，有

$$\frac{\partial MSE}{\partial b}=2\left(mb-\sum_{i=1}^m(y^{(i)}-\mathbf{w}\mathbf{x}^{(i)})\right)$$

令梯度等于零，即可求解参数的最优解$w_,b_$。

多元线性回归

更一般地，我们把刚才的数据集表示为矩阵

$$X = \begin{bmatrix} x_{11} & x_{12} & ... & x_{1d} & 1 \\ x_{21} & x_{22} & ... & x_{2d} & 1\\ ... & ... & ... & ... & ... \\ x_{m1} & x_{m2} & ... & x_{md} & 1 \end{bmatrix}=\begin{bmatrix} x_1^T & 1 \\ x_2^T & 1 \\ ... & ... \\ x_m^T & 1 \end{bmatrix}$$

标签记作

$$y=\begin{bmatrix} y_1 \\ y_2 \\...\\y_m \end{bmatrix}$$

同样地，我们对$\mathbf{w}$求梯度得到

$$\frac{\partial MSE}{\partial \mathbf{w}} = 2X^T(X\mathbf{w}-y)$$

令上式为零，得到参数最优解的解析解形式

$$\mathbf{w}_*=(X^TX)^{-1}X^Ty$$

逻辑回归

上面的问题是一般的回归问题，那些模型的输出可以是一定范围内的任意数；而有一些问题，比如分类问题，它要求模型的输出只能是几种类别中的一个。

以最简单的二分类问题为例，我们基于上面已经建立起来的线性模型推导出符合解决二分类问题的模型——最简单的做法其实是直接给原来的输出加上一个“分段函数”；我们常用Sigmoid函数来达到这个效果

$$Sigmoid(z)=\frac{1}{1+e^{-z}}$$

将z代换为原先的线性组合，得到适用于二分类问题的逻辑回归模型

$$g(x)=\frac{1}{1+e^{-(w^Tx+b)}}$$

接下来使用极大似然估计法来使得概率最大化。

线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA），也称“Fisher判别分析”，主要思想是，给定训练数据集情况下，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。

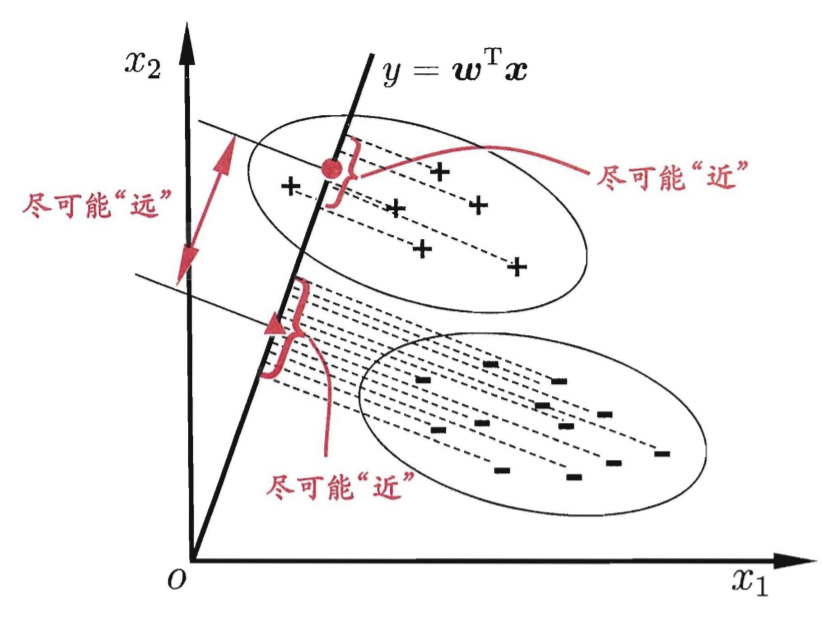
接下来，我们以简单的二分类问题，来逐步推导一下LDA的数学原理。

二分类LDA

为了方便讨论，约定

• $X_i$表示第i类样本点的集合
• $\mu_i$表示第i类样本点的均值向量
• $\mathbf{w}$表示直线的方向向量

另外，向量内积可以表示为$x·w=w^Tx$，其中$w,x\in \mathbb{R}^n$，而向量x在直线w上的投影则可以表示为$\displayst\frac{w^Tx}{||w||_2}$，也就是说，如果w模长为1，那么向量x在直线w上的投影就可以表示为$w^Tx$。为此，我们接下来都假设$||w||_2=1$。以下图为例进行简单说明。

$$\begin{aligned} &\mathbf{x}·\mathbf{w}=||\mathbf{x}||·||\mathbf{w}||·\cos\theta \\\\ &\Rightarrow \mathrm{Prj}_\mathbf{w}\mathbf{x} = ||\mathbf{x}||·\theta=\frac{\mathbf{x}·\mathbf{w}}{||\mathbf{w}||} \end{aligned}$$

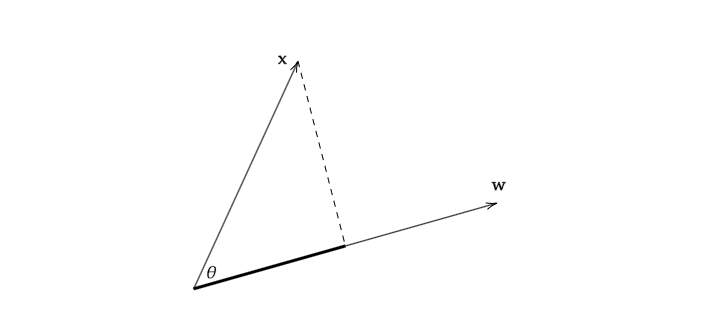
再回顾上面关于LDA的两条基本原则：

1. 同类样例的投影点尽可能接近
2. 异类样例的投影点尽可能远离

为了衡量这两条原则，引入了量化指标散度矩阵。

散度矩阵

先考虑类间散度矩阵。可以直接采用类的均值向量$\mu_i,i\in\{0,1\}$在直线上的投影距离$w^T\mu_i$，考虑如下量化标准

$$(w^T\mu_0-w^T\mu_1)^2=(w^T(\mu_0-\mu_1))^2=w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw$$

上式中，$(\mu_0-\mu_1)(\mu_0-\mu_1)^T$即为类间散度矩阵，记作$S_b$。

再考虑类内散度矩阵。与方差类似，我们考虑

$$D(X_i)=\sum_{x\in X_i}(w^Tx-w^T\mu_i)^2,\ i\in \{0,1\}$$

进而有如下量化标准

$$\begin{aligned} \sum_{i=0}^1D(X_i)&=\sum_{i=0}^1\sum_{x\in X_i}(w^Tx-w^T\mu_i)^2\\\\ &=w^T\sum_{i=0}^1\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^Tw \end{aligned}$$

上式中，$\displaystyle \sum_{i=0}^1\sum_{x\in X_i}(x-\mu_0)(x-\mu_0)^T$即为类内散度矩阵，记作$S_w$。

综上，有定义

• 类间散度矩阵$S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T \in \mathbb{R}^{n\times n}$
• 类内散度矩阵$S_w=\displaystyle \displaystyle \sum_{i=0}^1\sum_{x\in X_i}(x-\mu_0)(x-\mu_0)^T\in \mathbb{R}^{n\times n}$

目标函数与拉格朗日法求解优化问题

我们的目标函数被称为广义瑞利商，最大化之即可。

$$\begin{aligned} &\max J \\\\ &J=\frac{\mathbf{w}^TS_b\mathbf{w}}{\mathbf{w}^TS_w\mathbf{w}} \end{aligned}$$

经过观察，$J$的取值与$\mathbf{w}$的模长无关。因此，令$w^TS_ww=1$，我们将原问题转化为如下的优化问题：

$$\begin{aligned} &\max_\mathbf{w} \mathbf{w}^TS_b\mathbf{w}\\\\ &s.t.\mathbf{w}^TS_w\mathbf{w}=1 \end{aligned}$$

这是一个很典型的约束优化问题，可以用拉格朗日乘子法求解。

$$L(w,\lambda)=-\mathbf{w}^TS_b\mathbf{w}+\lambda(\mathbf{w}^TS_w\mathbf{w}-1)$$

其中$\lambda$即为拉格朗日乘子。对$\mathbf{w}$求偏导数得

$$\frac{\partial L(\mathbf{w},\lambda)}{\partial \mathbf{w}}=-2S_b\mathbf{w}+2\lambda S_w\mathbf{w}$$

令上式等于零，得到

$$S_b\mathbf{w}_*=\lambda S_w\mathbf{w}_*$$

再结合先前的式子

$$S_b\mathbf{w}_*=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\mathbf{w}_*$$

得到

$$\lambda S_w\mathbf{w}_*=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\mathbf{w}_*$$

我们并不关心w的模长，只关心它的方向，而$(\mu_0-\mu_1)^T\mathbf{w}_*$是一个标量，不妨记作k，因此有

$$\mathbf{w}_*=\frac{k}{\lambda}S_w^{-1}(\mu_0-\mu_1)$$

舍去标量系数，仅保留其中的方向信息，得

$$\mathbf{w}_*=S_w^{-1}(\mu_0-\mu_1)$$

这便是直线的方向向量。

直接求解

事实上，如果要直接求解优化问题

$$\begin{aligned} &\max J \\\\ &J=\frac{\mathbf{w}^TS_b\mathbf{w}}{\mathbf{w}^TS_w\mathbf{w}} \end{aligned}$$

也是可行的。毕竟上面的解法忽略了$\mathbf{w}$的模长而只考虑了其方向。首先对$J$求关于$\mathbf{w}$的梯度

$$\begin{aligned} \nabla_\mathbf{w}J &= \frac{2S_b\mathbf{w}(\mathbf{w}^TS_w\mathbf{w})-2(\mathbf{w}^TS_b\mathbf{w})S_w\mathbf{w}}{(\mathbf{w}^TS_w\mathbf{w})^2}\end{aligned}$$

令上式等于0，整理得

$$\begin{aligned} S_b\mathbf{w}(\mathbf{w}^TS_w\mathbf{w})-(\mathbf{w}^TS_b\mathbf{w})S_w\mathbf{w}&=0 \\\\ S_b\mathbf{w}(\mathbf{w}^TS_w\mathbf{w}) &= (\mathbf{w}^TS_b\mathbf{w})S_w\mathbf{w}\\\\ S_b\mathbf{w} &= \frac{\mathbf{w}^TS_b\mathbf{w}}{\mathbf{w}^TS_w\mathbf{w}}S_w\mathbf{w} \\\\ S_w^{-1}S_b\mathbf{w} &= \lambda \mathbf{w} \end{aligned}$$

这里记$\displaystyle \lambda=J=\frac{\mathbf{w}^TS_b\mathbf{w}}{\mathbf{w}^TS_w\mathbf{w}}$，实际上将原优化问题转化为了求解$S_w^{-1}S_b$的最大特征值的问题。而$\mathbf{w}$就是该特征值对应的特征向量。

多类LDA

和上面的二类问题类似地，我们有由$m$个样本组成的数据集

$$\mathrm{D}=\{ (\mathbf{x}^{(1)},y^{(1)}), (\mathbf{x}^{(2)}, y^{(2)}), \cdots,(\mathbf{x}^{(m)}, y^{(m)}) \}$$

其中，$\mathbf{x}^{(i)}\in\mathbb{R}^n$数据集$\mathrm{D}$共包含$k$个类别，每一个类别包含的样本数量为$N_i,i\in \{1,2,\cdots, k\}$，所包含的样本集合记作$X_i$，且该类别样本均值为$\displaystyle \mu_i=\frac{1}{N_i}\sum_{j=1}^{N_i}X_i^{(j)}$，样本的协方差矩阵记作$\displaystyle \Sigma_i=\sum_{\mathbf{x}^{(j)}\in X_i}(\mathbf{x}^{(j)}-\mu_i)(\mathbf{x}^{(j)}-\mu_i)^T$。

和二类问题有差异的是，此时的低维空间不一定就是一条直线，而是一个空间，不妨设为$d$维空间。那么这时就需要利用到该$d$维空间的一组基$\{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_d\}$了。将这组基拼接起来写成矩阵

$$W_{n\times d}=[\mathbf{w}_1, \mathbf{w}_2, \cdots, \mathbf{w}_d]$$

先考虑类间散度矩阵。计算全部样本的均值$\displaystyle \mu=\frac{1}{m}\sum_{i=1}^m\mathbf{x}^{(i)}$，类间散度矩阵表示为

$$S_b=\sum_{i=1}^k N_i\left( \mu_i-\mu \right)(\mu_i - \mu)^T$$

类内散度矩阵表示为

$$S_w=\sum_{i=1}^k \Sigma_i = \sum_{i=1}^k \sum_{\mathbf{x}^{(j)}\in X_i}\left( \mathbf{x}^{(j)}-\mu_i \right)\left( \mathbf{x}^{(j)}-\mu_i \right)^T$$

如果按照二类LDA的做法，我们应该得到优化问题

$$\max_W \frac{W^TS_bW}{W^TS_wW}$$

但是，上式中的分子、分母均为矩阵而不是标量，因此无法按照二类LDA的求解方法进行优化。所幸的是，我们却可以使用其他的一些优化函数进行等价的替代，比如

$$\begin{aligned} J(W)&=\frac{\displaystyle \prod_{diag}W^TS_bW}{\displaystyle \prod_{diag}W^TS_wW} \\\\ &= \frac{\displaystyle \prod_{i=1}^d\mathbf{w}_i^TS_b\mathbf{w}_i}{\displaystyle \prod_{i=1}^d\mathbf{w}_i^TS_w\mathbf{w}_i} \\\\ &=\prod_{i=1}^d\frac{\mathbf{w}_i^TS_b\mathbf{w}_i}{\mathbf{w}_i^TS_w\mathbf{w}_i} \end{aligned}$$

进而转化为优化问题

$$\max J(W)$$

而事实上，$J(W)$形式中出现了之前提到过的广义瑞利商，问题也就可以按照二类LDA优化方法求解了。

类别不平衡问题

当训练数据集中不同类别的样例数目有差别时，会对学习造成影响。比如正例太少、反例太多。解决类别不平衡学习的基本策略为再平衡：

不妨以线性模型为例

$$y=\mathbf{w}^T\mathbf{x}+b$$

假设输出结果$y>0.5$时判别为正例，否则判别为反例，也即分类器的决策规则为

$$\frac{y}{1-y}>1，预测为正例$$

但是由于数据集类别不平衡学习，希望分类器执行的决策为

$$\frac{y}{1-y}>\frac{m^+}{m^-}，预测为正例$$

其中$\frac{m^+}{m^-}$为观测几率，是数据集中正例数量与反例数量之比；也就是说只要高于该值，就表示为正例。

所以再平衡策略就是对预测值进行调整：

$$\frac{y'}{1-y'}=\frac{y}{1-y}\times \frac{m^-}{m^+}$$

赏