主成分分析

主成分分析是一种使用极为广泛的数据降维方法，比如，给定一组m维数据，可以利用主成分分析，将这组数据降为n维数据，其中$n<m$。

从最简单的例子谈起

为了使得主成分分析原理更加直观，当然选择维度为2的情况进行说明：考虑平面上的5个点，我们现在准备将其降维成1维样本点，也即将二维样本点投影到某条直线上。

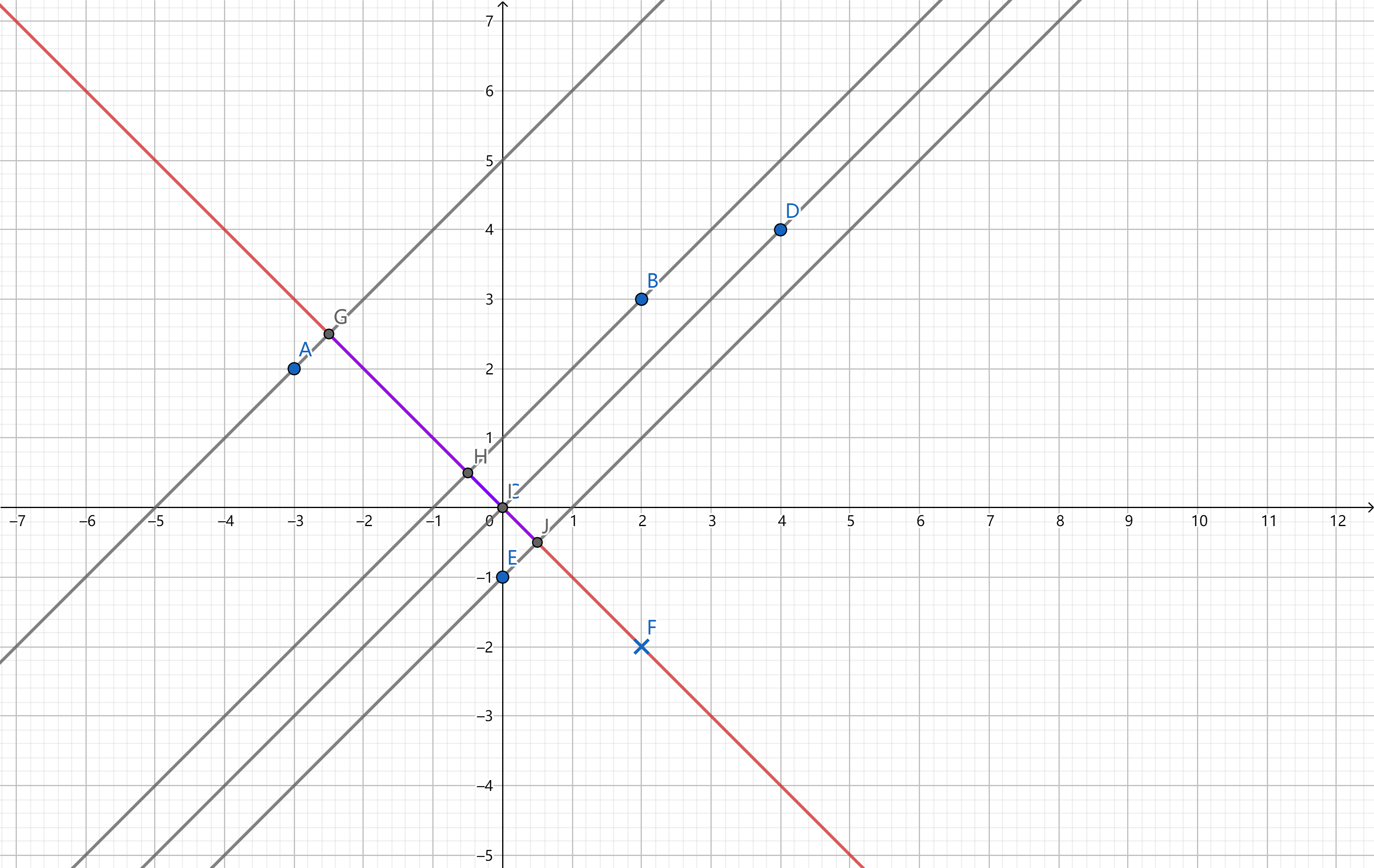
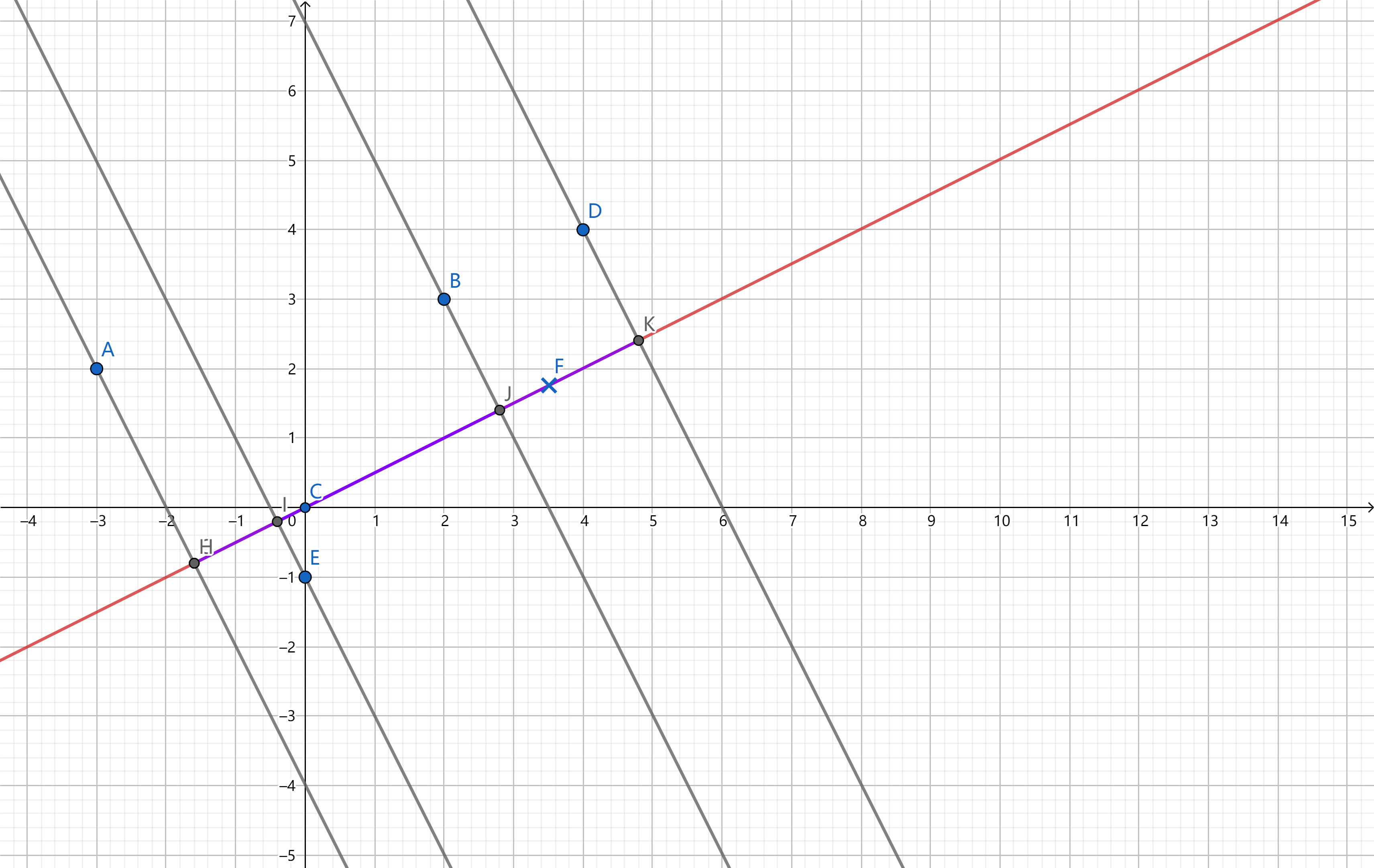
下图是给定的两条直线，两种情况下，原始二维样本点均为A、B、C、D、E；

• 第一种情况下，降维后的投影点为G、H、C、J
• 第二种情况下，降维后的投影点为H、I、J、K

为了方便讨论，将投影定义为投影点到原点的距离，已在图中用紫色线段标出。

给出的两条直线，哪一条直线上的投影更好呢？我们直观感受到，第二种情况效果更好。实际上，相比于第一种情况，第二种情况下，二维点在直线上的投影方差最大，更具有代表性。

因此，我们从投影方差角度理解主成分分析：

要把m维数据降维至n维，就需要找到n个互相正交的方向轴，使得原m维数据每一个方向上的投影的方差达到最大。其中，$n<m$。

数学推导

给定k个样本点，每一个样本点$z^{(i)} \in \mathbb{R}^m$维度均为m，记作Z=$(\mathbf{z}^{(1)},\mathbf{z}^{(2)} ,…,\mathbf{z}^{(k)} )$，下面进行数学推导。

注意：此处的$\mathbf{z}^{(i)}$以及下文的$\mathbf{x}^{(i)}, \mathbf{u}_i, \xi_{i}$均为列向量。

首先进行中心化，计算均值$\mu=\frac{1}{n}\sum_{i=1}^kz^{(i)}$，中心化之后的样本点即为

$$\mathbf{x}^{(i)} = \mathbf{z}^{(i)} - \mu$$

我们先找第一主轴$u_1$。考虑各个样本点$x_i$在第一主轴上的投影，当方差最大时，也即投影的绝对值最大：

$$\max_{\mathbf{u}_1}\frac{1}{n}\sum_{i=1}^k|\mathbf{x}^{(i)}·\mathbf{u}_1|$$

此处的·表示向量内积，而向量内积表示投影的大小。

等价地，我们只需求如下式子的最大值：

$$\begin{aligned} \sum_{i=1}^k(\mathbf{x}^{(i)}·\mathbf{u}_1)^2&=\sum_{i=1}^k(\mathbf{x}^{(i)T}\mathbf{u}_1)^2\\\\ &=\sum_{i=1}^k(\mathbf{x}^{(i)T}\mathbf{u}_1)^T(\mathbf{x}^{(i)T}\mathbf{u}_1)\\\\ &=\sum_{i=1}^k\mathbf{u}_1^T\mathbf{x}^{(i)}\mathbf{x}^{(i)T}\mathbf{u}_1\\\\ &=\mathbf{u}_1^T(\sum_{i=1}^k\mathbf{x}^{(i)}\mathbf{x}^{(i)T})\mathbf{u}_1 \end{aligned}$$

记$X=(\mathbf{x}^{(1)},\mathbf{x}^{(2)},…,\mathbf{x}^{(k)})$，则等价变换为

$$\mathbf{u}_1^TXX^T\mathbf{u}_1$$

这是一个二次型。我们接下来求解这个目标式子的最大值，以及$\mathbf{u}_1$取何值时达到最大值。

求最大值

$$\begin{aligned} &\max_{\mathbf{u}_1}\mathbf{u}_1^TXX^T\mathbf{u}_1\\\\ \Rightarrow &\max_{\mathbf{u}_1}(X^T\mathbf{u}_1)^T(X^T\mathbf{u}_1)\\\\ \Rightarrow &\max_{\mathbf{u}_1}||X^T\mathbf{u}_1||_2^2\\\\ \Rightarrow &\max_{\mathbf{u}_1}\left(\frac{||X^T\mathbf{u}_1||_2}{||\mathbf{u}_1||_2}\right)^2 \end{aligned}$$

对于矩阵X，它对一个向量$u_1$做变换，前后向量的模长之比的最大值，其实就是矩阵X的最大奇异值。

因此我们得到目标式子的最大值：

$$\mathbf{u}_1^TXX^T\mathbf{u}_1=\left(\frac{||X^T\mathbf{u}_1||_2}{||\mathbf{u}_1||_2}\right)^2\leqslant \sigma_{max}(X)$$

求第一主轴

何时取等号呢？

我们设对称矩阵$XX^T$有$k$个特征值

$$\lambda_1,\lambda_2,...,\lambda_k$$

相应地，有$k$个特征向量

$$\xi_1,\xi_2,...,\xi_k$$

$k$个特征向量两两正交，可以作为一组标准正交基。

对于任意一个向量$\mathbf{x}$，可以表示为

$$\mathbf{x}=\sum_{i=1}^k\alpha_i\xi_i$$

故而有

$$||\mathbf{x}||_2^2=(\alpha_1,\alpha_2,...,\alpha_k)·(\alpha_1,\alpha_2,...,\alpha_k)=\sum_{i=1}^k\alpha_i^2$$ $$||A\mathbf{x}||_2^2=(A\mathbf{x})^T(A\mathbf{x})=\mathbf{x}^TA^TA\mathbf{x}=\mathbf{x}·(A^TA\mathbf{x})=\left(\sum_{i=1}^k\alpha_i\xi_i\right)·\left(A^TA\sum_{i=1}^k\alpha_i\xi_i\right)$$

注意到$A^TA\xi_i=\lambda_i\xi_i$，进而得

$$\begin{aligned} ||A\mathbf{x}||_2^2 &=\left(\sum_{i=1}^k\alpha_i\xi_i\right)·\left(\sum_{i=1}^k\alpha_i\lambda_i\xi_i\right) \\\\ &=(\alpha_1,\alpha_2,...,\alpha_k)·(\alpha_1\lambda_1,\alpha_2\lambda_2,...,\alpha_k\lambda_k) \\\\ &=\sum_{i=1}^k\alpha_i^2\lambda_i \end{aligned}$$

假设特征值从大到小排列，即$\lambda_1\geqslant\lambda_2\geqslant\dots\geqslant\lambda_k$，得

$$||A\mathbf{x}||_2^2\leqslant\sum_{i=1}^k\alpha_i^2\lambda_1=\lambda_1||\mathbf{x}||_2^2$$

同样得到：

$$\frac{||A\mathbf{x}||_2}{||\mathbf{x}||_2}\leqslant\sqrt{\lambda_1}=\sigma_1$$

具体地，此处$\mathbf{u}_1$为最大特征值$\lambda_1$对应的特征向量方向。

求其他主轴

同理，其他的$\mathbf{u}_i$即为第i大的特征值$\lambda_i$对应的特征向量的方向。

算法流程

对于k个m维样本$X_{m\times k}=(x_1,x_2,…,x_k)$（即每一列均为一个样本），我们的目标是将其降到n维：

1. 将样本去中心化：

   $\forall x_i,x_i=x_i-\frac{1}{k}\sum_{j=1}^kx_j$

   $X’=(x_1,x_2,…,x_k)$

2. 计算样本的协方差矩阵

   $C_{m\times m}=\frac{1}{k}X’X’^T$

3. 求解出C的特征值和对应的特征向量

   $\lambda_1,\lambda_2,…,\lambda_k$($\lambda_1\geqslant\lambda_2\geqslant\dots\geqslant\lambda_k$)

   $\xi_1,\xi_2,…,\xi_k\in R^m$

4. 将特征向量按照对应特征值大小从上到下按行排列成矩阵，前n行组成矩阵P

   $P=(\xi_1,\xi_2,\dots,\xi_n)^T$

5. 降维

   $Y_{n\times k}=P_{n \times m}X_{m\times k}$

赏