二分法

算法简介

说到二分法，必须要提到的便是二分查找算法。

_Problem: Binary Search_

在一个严格递增序列A中寻找一个指定元素x，如果能找到，那么输出它的下标；如果不能找到，那么输出-1。

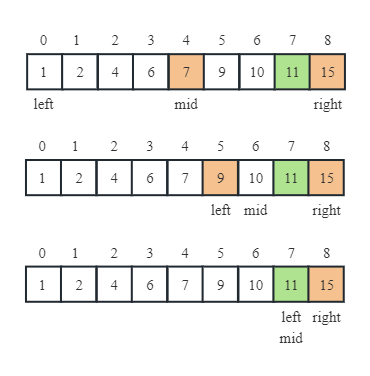
以在递增序列$[1,2,4,6,7,9,10,11,15]$中查找元素11为例，演示二分查找法的步骤。

int BinarySearch(int left, int right, int tgt) {
    // 在[left, right]中查找
    while(left < right) {
        int mid = left + (right - left) / 2;
        if(ns[mid] < tgt) {
            left = mid + 1;
        } else if(ns[mid] > tgt) {
            right = mid;
        } else return mid;
    }
    // 到这里，必有left==right，退化为
    if(ns[left] != tgt)	return -1; // 没找到
    return left;
}

另外，二分法也可以使用递归写法：

int BinarySearch(int left, int right, int tgt) {
    if(left == right) {
        // 如果区间退化为一个点，那么直接判断该点是否就是目标元素
        if(ns[left] != tgt)	return -1;
        else	return left;
    }
    // 递归
    int mid = left + (right - left) / 2;
    if(ns[mid] < tgt)	return BinarySearch(mid+1, right, tgt);
    else if(ns[mid] > tgt)	return BinarySearch(left, mid, tgt);
    else	return mid;
}

经典例题：旋转数组

旋转数组中的元素查找

问题链接：https://sunnywhy.com/sfbj/4/5/164

旋转数组是指，对一个给定的位置，将数组中该位置右侧（含该位置）的所有元素移至数组最左侧后形成的数组。例如[1,2,3,4,5]将元素3所在位置右侧的部分移到数组最前面后可以形成[3,4,5,1,2]，而将元素4所在位置右侧的部分移到数组最前面后可以形成[4,5,1,2,3]。

现在给定一个由严格递增序列形成的旋转数组A，在其中寻找一个元素x。如果存在，那么输出x所在的下标；否则输出-1。

不妨记序列为ns，而二分法逃不开中间元素ns[mid]，因此先考虑序列中的中间元素ns[mid]与整个序列的关系。假设严格递增序列形成的旋转数组ns为

稍加思索便可发现，ns一定由两段严格递增的序列拼接而成。也就是说，mid划分出来的两段子序列必有至少一侧是严格递增的（如果运气好，mid恰好就是连接点，比如上面例子的下标3，那么其两侧的子序列均为严格递增）。而只需判断ns[mid]是否大于ns[left]，如果大于，则左侧为严格递增子序列；反之亦然。判断出哪一侧严格递增后，进一步判断目标元素target是否在整个范围内，进行二分即可。

具体地，以ns[mid]>ns[left]即左侧为严格递增子序列为例有

• 若ns[left]<target<ns[mid]，则搜索区间变为$[left, mid]$；
• 否则，搜索区间变为$[mid+1, right]$

另外注意，应该单独考虑ns[mid]==target这种情况，因为这种情况直接得到答案，可以直接返回结果。

int binarySearch(int left, int right, int tgt) {
	// [5, 7, 8, 9, 1, 3]
	if(left == right)	return ns[left] == tgt ? left : -1;
	int mid = left + (right - left) / 2;
	if(ns[mid] == tgt)	return mid;
	
	if(ns[mid] < ns[right]) {
		// 旋转点一定在mid左侧，[mid, right]单调递增
		if(ns[mid] < tgt && tgt <= ns[right])	return binarySearch(mid+1, right, tgt);
		else	return binarySearch(left, mid, tgt);
	} else {
		// 旋转点一定在mid或者mid右侧，[left, mid]单调递增 
		if(ns[mid] > tgt && tgt >= ns[left])	return binarySearch(left, mid, tgt);
		return binarySearch(mid+1, right, tgt);
	}
}

旋转数组求原序列中位数

如何求出原严格递增序列的中位数？其实如果能够找出两个严格递增子序列的“拼接点”，问题便迎刃而解了：左侧子序列元素均大于右侧子序列元素，而两个子序列内部严格递增，此时只需要$\mathcal{O}(1)$时间便可求出中位数。于是关键在于求出拼接点。

和前一部分类似地，要进行二分，就要判断拼接点到底在左侧区间还是右侧区间。而根据“只需判断ns[mid]是否大于ns[left]，如果大于，则左侧为严格递增子序列；反之亦然”，拼接点不可能出现在严格递增子序列中，只可能出现在另一侧，于是可以得到如下代码：

int binarySearch(int left, int right) {
    while(left < right) {
        int mid = left + (right - left) / 2;
        // 如果满足ns[mid]>ns[mid+1]，那么mid就是拼接点下标
        if(ns[mid] > ns[mid+1])	return mid;
        if(ns[mid] > ns[left]) {
            // [left, mid]严格递增，拼接点只可能出现在[mid+1, right]
            left = mid + 1;
        } else {
            // [mid+1, right]严格递增，拼接点只可能出现在[left, mid]
            right = mid;
        }
    }
    // 此时必有left == right，退化为一个点，由于拼接点必然存在，因此直接返回
    return left;
}

得到拼接的下标后，根据序列长度奇偶性取出数组中中间元素便不难了。下面是完整的代码。

#include <iostream>
#include <vector> 
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
vector<int> ns;

int binarySearch(int left, int right) {
	while(left < right) {
		int mid = left + (right - left) / 2;
		if(ns[mid] > ns[mid+1])	return mid;
		if(ns[mid] > ns[left])	left = mid + 1;
		else	right = mid;
	}
	return left;
}

int main(int argc, char** argv) {
	int n;
	scanf("%d", &n);
	while(n--) {
		int a;
		scanf("%d", &a);
		ns.push_back(a);
	}
	int idx = binarySearch(0, ns.size()-1);
	if(ns.size() % 2) {
		printf("%.1lf", ns[(idx+1+ns.size()/2)%ns.size()]/1.0);
	} else {
		int tmp = (idx + ns.size()/2) % ns.size();
		printf("%.1lf", (ns[tmp] + ns[(tmp+1)%ns.size()])/2.0);
	}

	return 0;
}

To be continued…