支持向量机

算法背景

SVM有三宝：间隔、对偶、核技巧。

宝一：间隔

从间隔角度来看，支持向量机可以分为三种：

• 硬间隔支持向量机
• 软间隔支持向量机
• 核支持向量机

硬间隔SVM

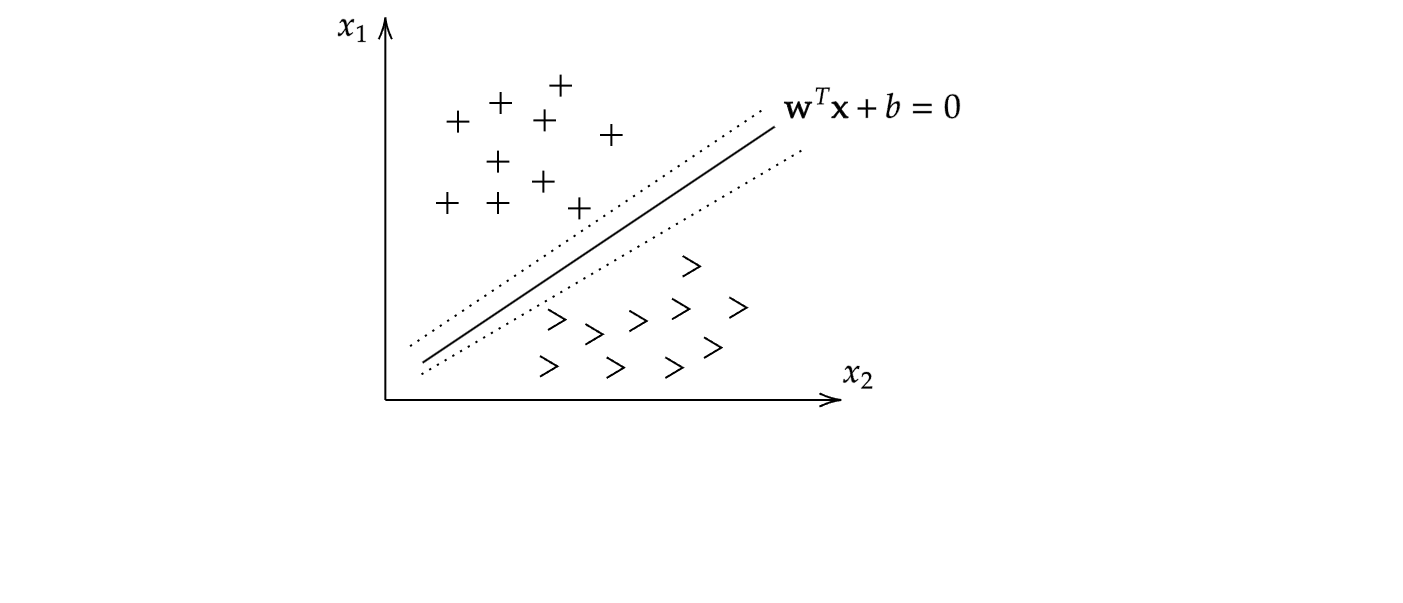
给定一组样本集合：$\{ (\mathbf{x}^{(1)}, y^{(1)}), (\mathbf{x}^{(2)}, y^{(2)}), \cdots, (\mathbf{x}^{(N)}, y^{(N)}) \}$，其中$\mathbf{x}^{(i)}\in \mathbb{R}^p, y^{(i)}\in \{-1,1\}$。

上图是二维数据情况下，支持向量机对样本的二分类的直观描述：找到一条超平面，将两类样本完全分开。而满足这个条件的超平面其实是有无数个的，究竟该选择哪一个呢？有如下限制：选取间隔最大的超平面，它恰好能够将不同类别完全分开。

我们先将“间隔”按下不表，来用简洁的数学语言描述一下最简单的支持向量机：

$$\begin{aligned} &\max \mathrm{margin}(\mathbf{w},b) \\\\ &s.t. (\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)} > 0 \end{aligned}$$

注意这里我们将条件

$$\begin{cases} \mathbf{w}^T\mathbf{x}^{(i)}+b>0, y^{(i)}=1 \\\\ \mathbf{w}^T\mathbf{x}^{(i)}+b<0, y^{(i)}=-1 \end{cases}$$

统一成一个

$$(\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)} > 0$$

接下来我们关注一下所谓的“间隔”$\mathrm{margin}$。间隔实际上指的是所有的点到该超平面的距离（$\mathrm{dis}$）的最小值。由点到直线距离公式，可知样本$(\mathbf{x}^{(i)},y^{(i)})$到超平面$\mathbf{w}^T\mathbf{x}+b=0$的距离为

$$\mathrm{dis}^{(i)} = \frac{|\mathbf{w}^T\mathbf{x}^{(i)}+b|}{||\mathbf{w}||}$$

借助标签，进一步将$\mathrm{dis}$绝对值去除：

$$\mathrm{dis}^{(i)} = \frac{(\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)}}{||\mathbf{w}||}$$

故支持向量机描述为：

$$\begin{aligned} &\max_{\mathbf{w},b}\min_{i} \frac{(\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)}}{||\mathbf{w}||} \\\\ &s.t. (\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)} > 0 \end{aligned}$$

接下来我们继续推导目标函数，将形式简化：

$$\max_{\mathbf{w},b}\frac{1}{||\mathbf{w}||}\min_{i}y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)$$

这个式子很有意思。首先一定有

$$\exists \gamma > 0, s.t.\gamma=\min_iy^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)$$

事实上，$\gamma$取值并不重要，因为对$\mathbf{w},b$的等比例缩放并不会影响到其所表示的超平面，换言之，下面两个超平面其实是完全等价的：

$$\begin{cases} \mathbf{w}^T\mathbf{x}^{(i)}+b=0 \\\\ \frac{\mathbf{w}^T}{\gamma}\mathbf{x}^{(i)} + \frac{b}{\gamma}=0 \end{cases}$$

因此，为方便后续运算，令$\gamma=1$，进而得到待优化的目标函数与约束条件

$$\begin{aligned} &\max_{\mathbf{w},b}\frac{1}{||\mathbf{w}||} \\\\ &s.t.(\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)} \geqslant 1 \end{aligned}$$

而通常我们习惯求解最小优化问题，于是最终的支持向量机描述为

$$\begin{aligned} &\min_{\mathbf{w},b} \frac{||\mathbf{w}||}{2} \\\\ &s.t. (\mathbf{w}^T\mathbf{x}^{(i)}+b)y^{(i)} \geqslant 1 \end{aligned}$$

接下来我们尝试求解这个带约束优化问题。

求解约束优化问题

对于约束优化问题，引入拉格朗日函数，将其转化为无约束优化问题：

$$\begin{aligned} &\min_{\mathbf{w},b}\max_{\Lambda}\mathcal{L}(\mathbf{w},b,\Lambda) \\\\ &s.t. \Lambda \geqslant 0 \end{aligned}$$

其中$\Lambda=[\lambda_1,\lambda_2,\cdots,\lambda_N], \mathbf{w}=[w_1,w_2,\cdots,w_N]$

根据强对偶条件，该优化问题也可等价于：

$$\begin{aligned} &\max_{\Lambda}\min_{\mathbf{w},b}\mathcal{L}(\mathbf{w},b,\Lambda) \\\\ &s.t. \Lambda \geqslant 0 \end{aligned}$$

拉格朗日函数为

$$\mathcal{L}(\mathbf{w},b,\Lambda)=\frac{||\mathbf{w}||}{2} + \sum_{i=1}^N\lambda_i(1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b))$$

关于约束优化问题(8)(9)(10)之间的等价性，下面从逻辑分析角度进行简单的分析（并非严格的数学证明）。

(9)到(8)

相比于(8)，(9)实际上是一个无约束问题。我们分别考虑下面两种情况：

1. $\exists i \in \{1,2,\cdots,N\}, s.t. 1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)>0$
2. $\forall i \in \{1,2,\cdots,N\}, 1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b) \leqslant 0$

对于第一情况，显然取$\lambda_i=\infty$，有

$$\max_{\Lambda}\mathcal{L}(\mathbf{w},b,\Lambda) = \infty$$

对于第二种情况，显然取$\Lambda=\mathbf{0}$，有

$$\max_{\Lambda}\mathcal{L}(\mathbf{w},b,\Lambda)=\frac{||\mathbf{w}||}{2}$$

综上有

$$\min_{\mathbf{w},b}\max_{\Lambda}\mathcal{L}(\mathbf{w},b,\Lambda)=\min_{\mathbf{w},b}\left\{ \infty, \frac{||\mathbf{w}||}{2} \right\}=\min_{\mathbf{w},b}\frac{||\mathbf{w}||}{2}$$

换言之，(9)通过改变待优化目标函数的形式，将(8)中的约束条件隐式地包含了，故而不再需要额外的约束条件。

(9)和(10)

这两个约束优化问题互为对偶问题。且此时待优化函数是凸函数，满足强对偶条件，因此它们等价。

对偶问题

原问题DP如下

$$\max_{\mathbf{w},b}\min_i \mathcal{L}(\mathbf{w},b,\Lambda)$$

其对偶问题LP为

$$\min_i\max_{\mathbf{w},b}\mathcal{L}(\mathbf{w},b,\Lambda)$$

记DP问题的最优解为$d^$，LP问题的最优解为$p^$，则有

$$d^*\leqslant p^*$$

上式也称为弱对偶条件。

而当约束函数为凸函数时，有$d^=p^$，此时称为强对偶。

求解最小优化问题

我们对优化问题(10)进行求解：

$$\begin{aligned} &\max_{\Lambda}\min_{\mathbf{w},b}\mathcal{L}(\mathbf{w},b,\Lambda) \\\\ &s.t. \Lambda \geqslant 0 \end{aligned}$$

其中

$$\mathcal{L}(\mathbf{w},b,\Lambda)=\frac{||\mathbf{w}||}{2} + \sum_{i=1}^N\lambda_i(1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b))$$

先求解最小优化问题：显然只需对$\mathbf{w},b$求偏导即可。

$$\begin{aligned} \frac{\partial \mathcal{L}}{\partial \mathbf{w}} &= \mathbf{w} - \sum_{i=1}^N\lambda_iy^{(i)}\mathbf{x}^{(i)} \\\\ \frac{\partial \mathcal{L}}{\partial b} &= -\sum_{i=1}^N \lambda_iy^{(i)} \end{aligned}$$

令偏导数为零，得到

$$\begin{aligned} &\mathbf{w}^*= \sum_{i=1}^N \lambda_iy^{(i)}\mathbf{x}^{(i)} \\\\ &\sum_{i=1}^N\lambda_iy^{(i)}=0 \end{aligned}$$

接下来，将上式代入$\mathcal{L}$，整理得

$$\begin{aligned} \min_{\mathbf{w},b} \mathcal{L}(\mathbf{w},b,\Lambda) &= \frac{||\sum_{i=1}^N \lambda_iy^{(i)}\mathbf{x}^{(i)}||}{2} - \sum_{i=1}^N\lambda_iy^{(i)}\left( \sum_{j=1}^N\lambda_jy^{(j)}\mathbf{x}^{(j)} \right)^T\mathbf{x}^{(i)} + \sum_{i=1}^N\lambda_i \\\\ &= \frac{1}{2}\left( \sum_{i=1}^N \lambda_iy^{(i)}\mathbf{x}^{(i)} \right)^T\left( \sum_{i=1}^N \lambda_iy^{(i)}\mathbf{x}^{(i)} \right) - \sum_{i=1}^N\sum_{j=1}^N \lambda_i\lambda_jy^{(i)}y^{(j)}<\mathbf{x}^{(i)},\mathbf{x}^{(j)}> + \sum_{i=1}^N\lambda_i \\\\ &=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\lambda_i\lambda_jy^{(i)}y^{(j)}<\mathbf{x}^{(i)},\mathbf{x}^{(j)}> - \sum_{i=1}^N\sum_{j=1}^N\lambda_i\lambda_jy^{(i)}y^{(j)}<\mathbf{x}^{(i)},\mathbf{x}^{(j)}> + \sum_{i=1}^N\lambda_i \\\\ &= -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\lambda_i\lambda_jy^{(i)}y^{(j)}<\mathbf{x}^{(i)},\mathbf{x}^{(j)}> + \sum_{i=1}^N\lambda_i \end{aligned}$$

到这里，我们得到如下等价的优化问题：

$$\begin{aligned} &\max_{\Lambda} -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\lambda_i\lambda_jy^{(i)}y^{(j)}<\mathbf{x}^{(i)},\mathbf{x}^{(j)}> + \sum_{i=1}^N\lambda_i \\\\ &s.t. \Lambda\geqslant 0 \\\\ & \quad \sum_{i=1}^N\lambda_iy^{(i)}=0 \end{aligned}$$

KKT条件

转化到上述优化问题后，可以通过一些特定软件求解参数$\lambda_1,\lambda_2,\cdots,\lambda_N$，进而将该问题解决。下面介绍另一部分非常重要的内容：KKT条件。

由于带约束优化问题满足强对偶，因此它满足KKT条件。而KKT条件包括原始可行性、对偶可行性和互补松弛条件，即

$$\begin{aligned} \nabla_\mathbf{w}\mathcal{L}=\nabla_{b}\mathcal{L}=0 \\\\ \lambda_i(1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)) = 0 \\\\ \Lambda \geqslant 0 \\\\ 1-y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b) \leqslant 0 \end{aligned}$$

上述条件中，第一个式子在前文已经利用到，得到的结果即(21)。下面来思考一下第二个式子的含义：事实上，第二个式子（互补松弛条件）揭示了这样的一个真相：只有位于超平面$\mathbf{w}^T\mathbf{x}+b=1$和$\mathbf{w}^T\mathbf{x}+b=-1$上的样本点才对优化目标函数的值产生了影响（否则对应的拉格朗日乘子$\lambda_i$均为零）。多提一句，我们把这样的点称为支持向量，这正是算法模型名称的由来。

关于支持向量

事实上，我们前面通过限定函数间隔定义过几何间隔：也就是说，所有样本点中，与决策超平面$\mathbf{w}^T\mathbf{x}+b=0$最近的点与之距离为$\frac{1}{||w||}$。可以利用点到距离公式验证，这样的点（也即支持向量）所在超平面就是$\mathbf{w}^T\mathbf{x}+b=1$以及$\mathbf{w}^T\mathbf{x}+b=-1$。

那么，一定有

$$\exists k\in \{1,2,\cdots,N\}, s.t.\quad 1-y^{(k)}(\mathbf{w}^T\mathbf{x}^{(k)}+b)=0$$

故而有

$$\begin{aligned} y^{(k)}(\mathbf{w}^T\mathbf{x}^{(k)}+b)&=1 \\\\ \mathbf{w}^T\mathbf{x}^{(k)}+b&=y^{(k)} \\\\ b&=y^{(k)}-\mathbf{w}^T\mathbf{x}^{(k)} \end{aligned}$$

结合(21)，得到最终的最优解

$$\begin{aligned} \mathbf{w}^*&=\sum_{i=1}^N\lambda_iy^{(i)}\mathbf{x}^{(i)} \\\\ b^*&=y^{(k)}-\sum_{i=1}^N\lambda_iy^{(i)}\mathbf{x}^{(i)T}\mathbf{x}^{(k)} \end{aligned}$$

软间隔SVM

其实到这里，已经注意到了：上面的SVM实际上是找到一个最优的决策超平面将样本严格分开，因此它被称为硬间隔SVM。与之相对地，如果构建的SVM允许分类中出现一点点错误，以此来换取更好的泛化能力，这种模型则称为软间隔SVM。

在硬间隔SVM中，约束条件是严格的：

$$y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b) \geqslant 1$$

而软间隔的引入实际上是对原来的目标函数加上一个惩罚项。首先，上述约束条件被放松，不再严格要求成立。另外需要引入一个参数$\xi_i$用于衡量这种“犯错误的程度”，即当$y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)<1$时，

$$\xi_i= 1 - y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)$$

注意，$\xi_i \geqslant 0$。

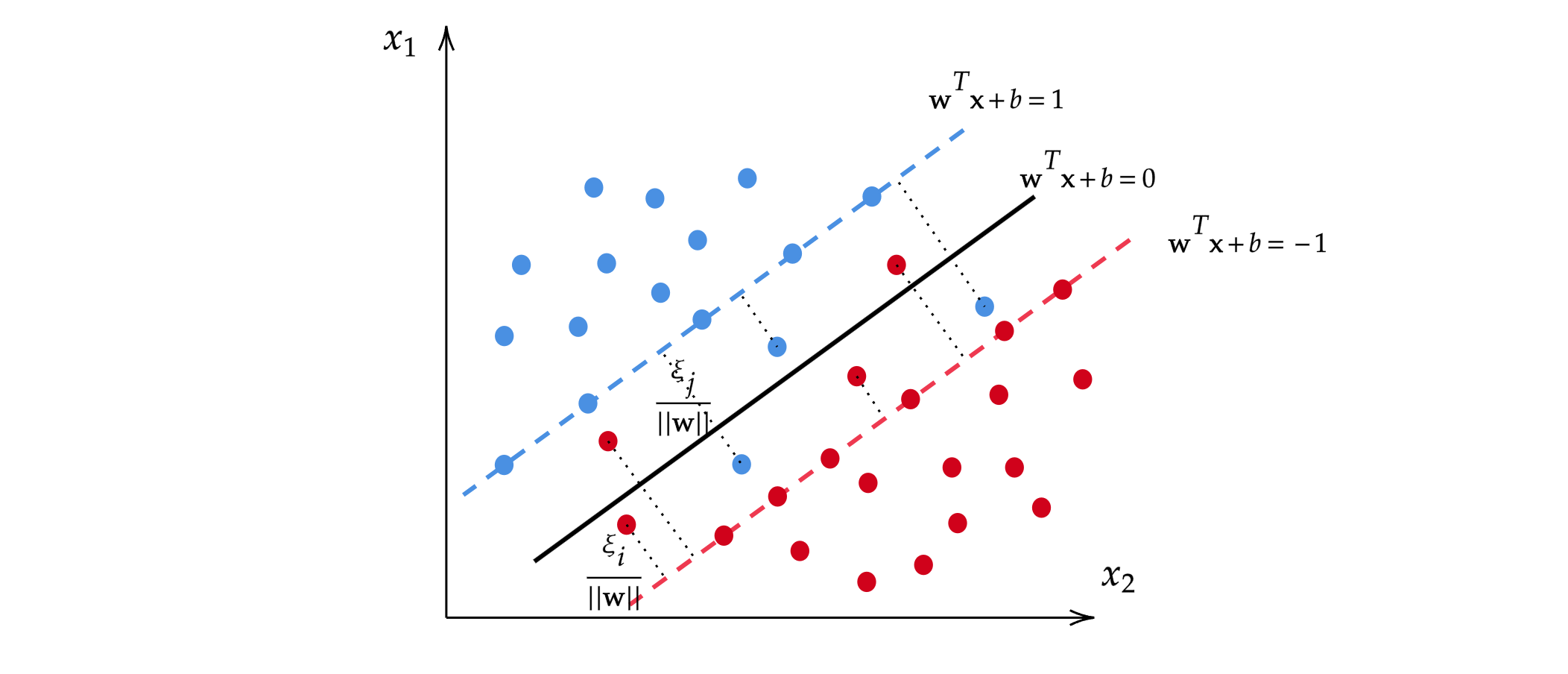
显然，$\xi_i$越大，表明样本“违反”原严格条件的程度越大，越应该受到惩罚。我们在原硬间隔SVM的目标函数基础上，添加一个带有惩罚系数$\mathcal{C}$的惩罚项，于是得到最终的软间隔SVM优化问题：

$$\begin{aligned} &\min_{\mathbf{w},b}\frac{1}{2}||\mathbf{w}||+\mathcal{C}\sum_{i=1}^N\xi_i \\\\ &s.t. y^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b) \geqslant 1-\xi_i \\\\ & \quad \quad \xi_i \geqslant 0 \end{aligned}$$

To be continued…

赏