平衡二叉树

背景

我们知道，一般来说，二叉查找树可以加快查找效率；但是如果一棵二叉查找树退化为了一根链（比如，除了叶子，每一个结点都只含有一个左孩子的树），查找起来也是相当的费劲，因为此时基本上就是遍历树中的每一个结点。这与我们使用树结构加快查找的初衷不符。事实上，我们正需要调整树的结构，使其成为平衡二叉树，这样查找起来效率较高。

定义

首先介绍一个概念：平衡因子。它是针对某一个结点而言的，指的是该结点左子树高度与右子树高度的差。值得注意的是，这个差并不是数学中严格意义上的两数之差——这个差是可正可负的。不难理解，平衡因子为负，则表示右子树高度比左子树高度要大一些。

那么平衡二叉树指的是这样的一种二叉树：它的每一个结点的平衡因子绝对值都不大于1。也就是说，若二叉树中每一个结点的左子树、右子树高度之差为-1、0或者1时，这棵树就是平衡二叉树了。

当然，平衡二叉树其实是特殊的二叉查找树。因此从代码实现角度看，与一般的二叉树定义不同的是，平衡因子必须出现在定义中，这也是方便后续的插入调整等操作。而通常我们将结点所在子树的高度保存到结点定义之中：

typedef struct s {
    int val;
    int height; // 以当前结点为根的子树的高度；若为叶子则就是1
    struct s* left;
    struct s* right;
} Node;

更新高度

既然平衡二叉树的定义中新增了height字段，因此在很多操作（如插入、建立等）中就会频繁地出现高度的更新且其不可或缺。由于插入操作是递归形式实现，因此我们定义的更新高度函数只需要简单的更新取该结点左子树和右子树高度较大值，加上1即可。然后这个操作会不断地随着递归的结束，自底向上的调用，从而保证了整棵树所有结点高度的更新。

注意，这里单独实现了获取结点高度的函数getHeight(Node* node)，是因为考虑结点为NULL的特殊情况，方便后续代码编写。

int getHeight(Node* node) {
    if(node == NULL)	return 0;
    return node->height;
}

void updateHeight(Node* root) {
    root->height = 1 + max(getHeight(root->left), getHeight(root->right));
}

插入操作

平衡二叉树最常见的知识点是插入操作。本文重点记录如何对平衡二叉树进行插入。显然，平衡二叉树其实是特殊的二叉查找树，每插入一个结点，就有可能“打破平衡”。因此关键在于，如何将这种非平衡的二叉树调整为平衡二叉树。

左旋、右旋

在正式介绍如何调整之前，我们来看如何调整当前的根结点。以下图为例，现在希望将根结点调整为$R’$，如何做？

为了有一个形象化的表述将整个调整过程描述出来，我们将$R$称为当前根结点（但是很快他就不是了），将$R’$称为新任根结点（他马上就是了），旧领导离任、新领导上任，是不是得有一套交接手续，才能完成权利的更迭？不妨按照这个路子理解接下来的调整过程。

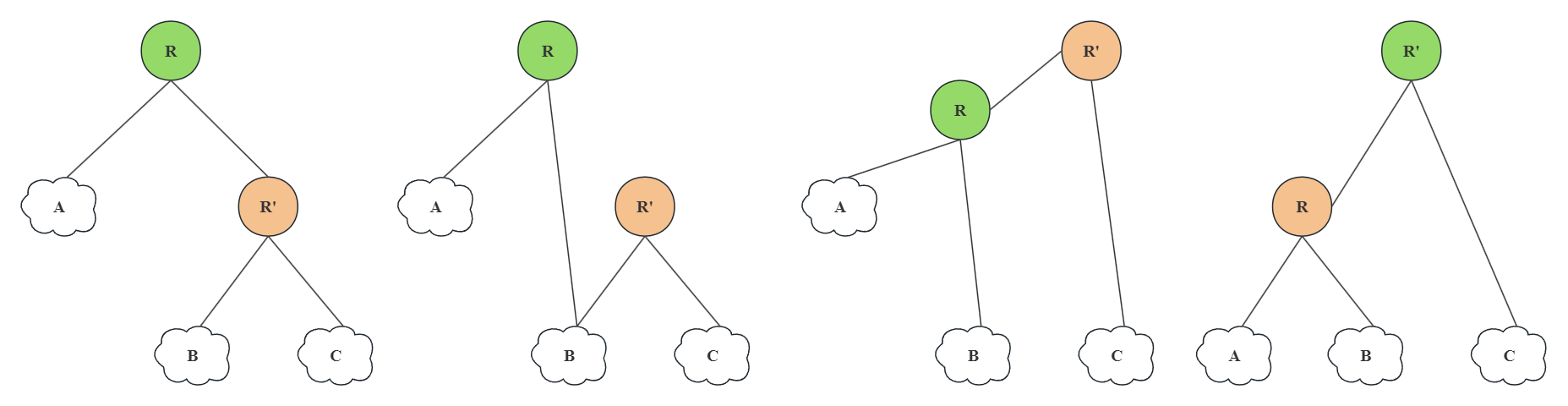
图中，云朵形框表示一棵子树结构，圆形框表示一个具体的结点；按照上图从左至右的顺序依次为：

1. 【旧任领导即将下台，新任领导即将上台】选中当前根结点和它的右结点；
2. 【旧任领导为下台做准备，接手新任领导手下的工作】当前根结点的右孩子指向它原先右孩子的左孩子；
3. 【新任领导为上台做准备，开始管理旧任领导】当前根结点成为其原先的右孩子的左孩子
4. 【交接完毕，权利更迭完成】原先的右孩子成为当前的最新根结点

这个调整过程，称为左旋。代码也很简单明了。只不过需要注意，在完成树中结点指针域的指向调整后，需要立即更新其高度（也就是当前根结点$R$和新任根结点$R’$，具体的更新操作前文已经有过说明）：

void leftRotate(Node* &root) {
    Node* temp = root->right;
    root->right = temp->left;
    temp->left = root;
    updateHeight(temp);
    updateHeight(root);
    root = temp;
}

与之相对地，是右旋操作。这是两个对称的操作过程，不再赘述。

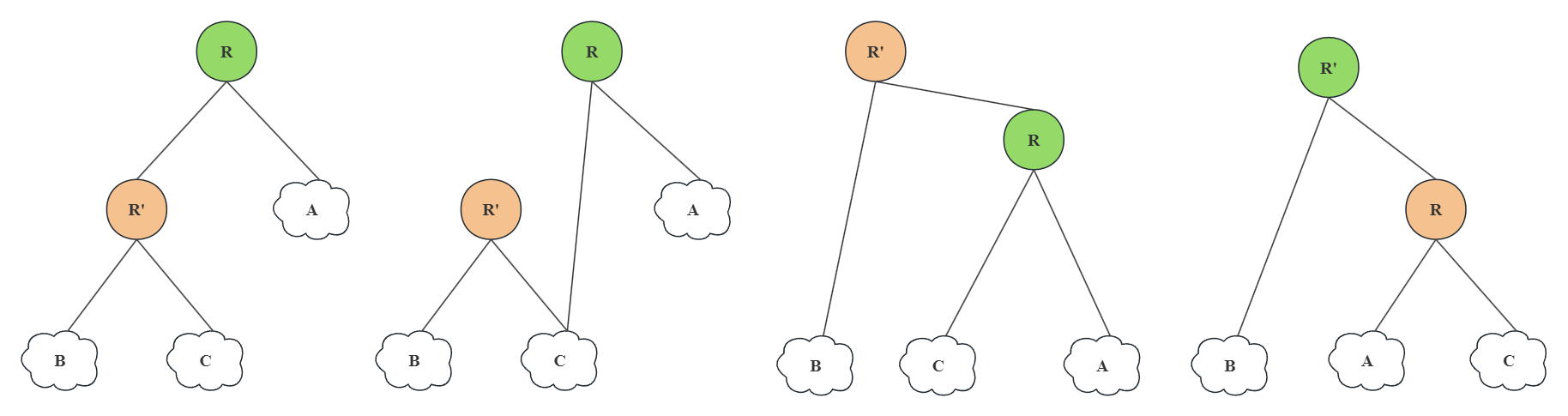
右旋代码如下。

void rightRotate(Node* &root) {
    Node* temp = root->left;
    root->left = temp->right;
    temp->right = root;
    updateHeight(temp);
    updateHeight(root);
    root = temp;
}

四种树型

有了上面的左旋、右旋基本操作后，接下来我们来看看针对几种不同的非平衡二叉树结构，该如何调整树型。

我们从根结点平衡因子角度考虑，当插入一个结点而导致树失衡时，一定导致某（几）个结点的平衡因子为2或者-2。不妨考虑平衡因子为2的情况，此时，以该结点为根的子树结构还可能有下面两种情况：

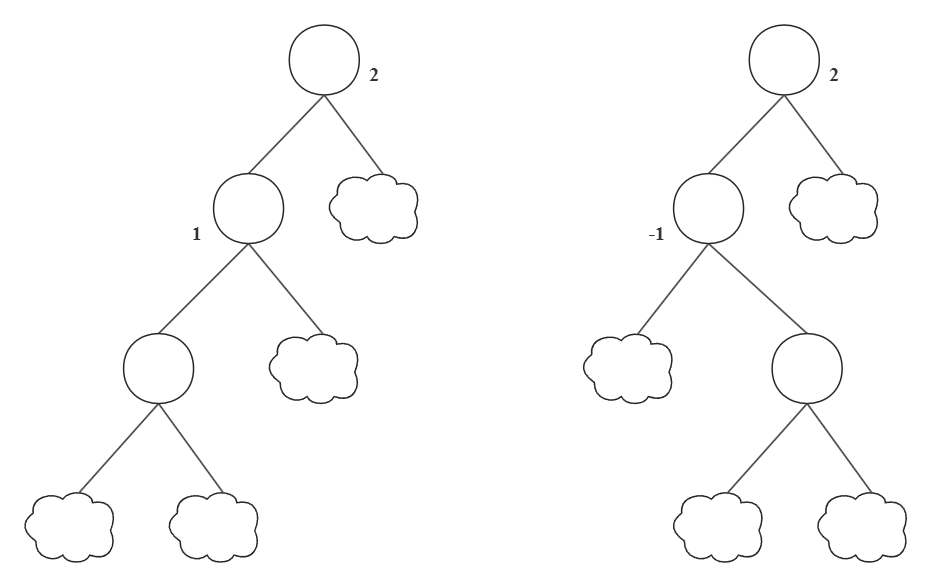
方便起见，记根结点为$R_1$，图中标出平衡因子为1或者-1的结点为$R_2$（$R_1$的左孩子）

• 对于上图左侧的LL型，处理方式比较简单，直接对$R_1$进行右旋即可，即调用rightRotate(R_1)；
• 对于右侧的LR型，则先对$R_1$的左孩子$R_2$进行左旋（此时忽略$R_1$），然后再对$R_1$进行右旋，即先调用leftRotate(R_1->left)，再调用rightRotate(R_1)。

根结点平衡因子为-2的情况与上面的情况对称，类似的有RR、RL型：

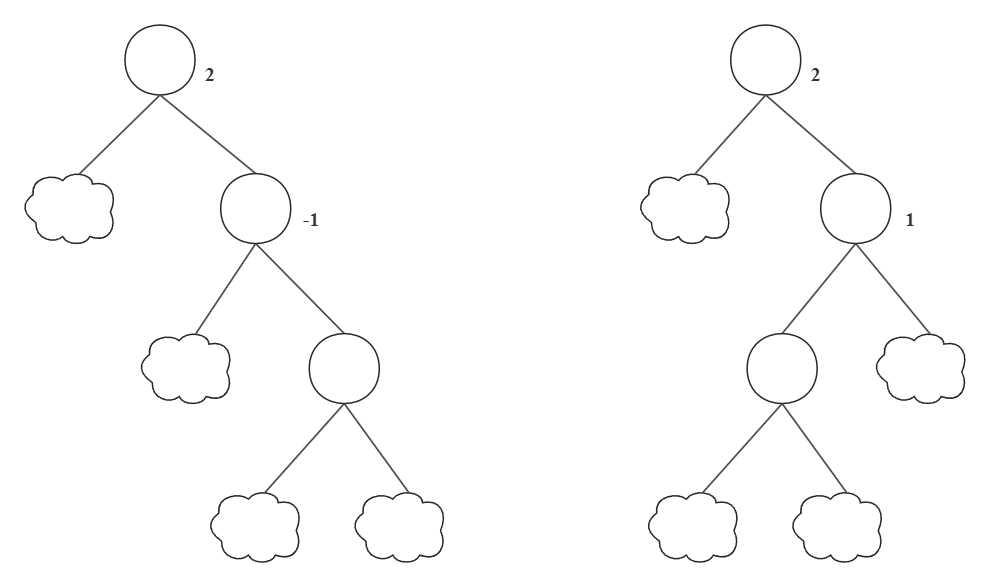
它们的调整方式不难推导出：

• 对于RR型，直接对根结点$R_1$进行左旋，即调用leftRotate(R_1)；
• 对于RL型，则先对根结点的右孩子$R_2$进行右旋（此时忽略根结点），然后再对根结点$R_1$进行左旋，即先调用rightRotate(R_1->right)，再调用leftRotate(R_1)。

完整代码

当然，目前我们已经知晓了几种不同失衡情况下的调整方法。那么，如何判断发生了失衡呢？很简单，只需要判断根结点的平衡因子是否为2或者-2，如果是则进一步判断其左孩子或者右孩子的平衡因子是否为1或者-1即可。于是，我们在写出完整的平衡二叉树插入结点之前，还需要编写获取某结点平衡因子的函数getBalancedFactor(Node* node)。

int getBalancedFactor(Node* node) {
    // 保证node不为NULL
    return getHeight(node->left) - getHeight(node->right);
}

插入操作的完整代码，可以看作在普通的二叉查找树上进行插入的代码基础上，进行了一番添加（毕竟二叉平衡树是特殊的二叉查找树）。

typedef struct s {
	int val, height;
	struct s* left;
	struct s* right;
} Node;

int getHeight(Node* root) {
	if(root == NULL)	return 0;
	return root->height;
}

void updateHeight(Node* root) {
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));
}

void leftRotate(Node* &root) {
	// 左旋root，当前根结点的右孩子为新任根结点 
	Node* rchild = root->right;
	root->right = rchild->left; // 当前根结点右孩子改为新任根结点的左孩子 
	rchild->left = root; // 新任根结点的左孩子改为当前根结点 
	updateHeight(root);
	updateHeight(rchild);
	root = rchild; // 新任根结点正式成为根结点 
}

void rightRotate(Node* &root) {
	// 右旋root，当前根结点的左孩子为新任根结点
	Node* lchild = root->left;
	root->left = lchild->right;
	lchild->right = root;
	updateHeight(root);
	updateHeight(lchild);
	root = lchild; 
}

int getBalancedFactor(Node* root) {
	return getHeight(root->left) - getHeight(root->right);
}

void insertNode(Node* &root, int val) {
	if(root == NULL) {
		Node* newNode = new Node();
		newNode->val = val;
		newNode->height = 1;
		newNode->left = newNode->right = NULL;
		root = newNode;
//		cout<<newNode->val<<" ";
		return;
	}
	if(val < root->val) {
        // 往左子树插入结点，此时根结点平衡因子可能为2（不可能为-2）
		insertNode(root->left, val);
        // 插入结点完成后，需要对当前的子树高度进行更新、调整（如果它不是平衡二叉树的话）；注意这是一个递归的过程，将随着递归的结束自底向上不断进行更新、调整，最终确保所有子树的高度正确无误、整棵树是平衡二叉树。
		updateHeight(root);
        
		if(getBalancedFactor(root) == 2) {
			// 左子树更高
			if(getBalancedFactor(root->left) == 1) {
				// LL
				rightRotate(root);
			} else if(getBalancedFactor(root->left) == -1) {
				// LR
				leftRotate(root->left);
				rightRotate(root);
			}
		}
	} else {
		insertNode(root->right, val);
        // 插入结点完成后，需要对当前的子树高度进行更新、调整（如果它不是平衡二叉树的话）；注意这是一个递归的过程，将随着递归的结束自底向上不断进行更新、调整，最终确保所有子树的高度正确无误、整棵树是平衡二叉树。
		updateHeight(root);
		
		if(getBalancedFactor(root) == -2) {
            // 往右子树插入结点，此时根结点平衡因子可能为-2（不可能为2）
			if(getBalancedFactor(root->right) == -1) {
				// RR
				leftRotate(root);
			} else if(getBalancedFactor(root->right) == 1) {
				// RL
				rightRotate(root->right);
				leftRotate(root);
			}
		}
	}
}