定义
并查集是一种特殊的数据结构,用于处理不相交集合的查询问题。实际上包含了三个操作:
- 合并:将不相交的两个集合合并为同一个集合
- 查找:查找元素所在的集合
算法核心
本文主要介绍并查集的算法模板。我们从并查集的常见操作入手,看看它的算法思想。
$\mathrm{father[]}数组$
在并查集中,我们通过维护一个保存当前元素父亲的数组father,来实现将属于不同集合的元素划分开。
比如,给定6个元素,它们的father数组为:father[6] = {0, 0, 0, 2, 4, 4},对应的元素分布情况见下图。
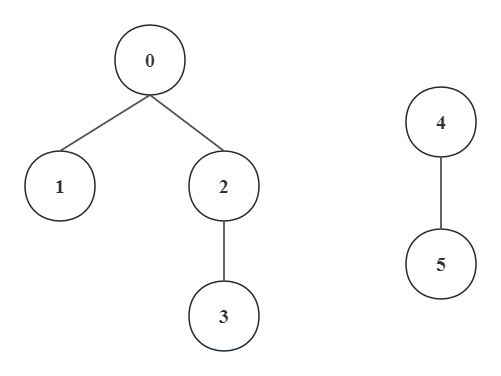
显然,这样表示下的集合总有一个“根结点”,且对于任意根结点$i$,它满足关系$\mathrm{father[i]=i}$。那么接下来我们来实现如何查找当前根结点。
查找
查找根结点,其实也就是不断地找父结点的父结点,直到满足了“父结点就是自己”这一终止条件。因此,我们可以使用递归很简单地实现。
int Find(int x) {
/*功能:查找结点x所在集合的根*/
if(x == father[x]) return x; // 终止条件:x就是根结点,直接返回
return Find(father[x]); // 递归:找父结点的父结点
}路径压缩
我们在平衡二叉树的引入中曾经提过,由于普通的二叉查找树可能由于呈现链状而使得查询效率变得很低;事实上,此处的并查集也可能出现类似的问题:

比如上图中,我们要查询5号的根结点,就需要调用Find(5),进而调用Find(4)、Find(3)、Find(2)、Find(1)、Find(0),才终于找到根结点0并返回。
而与上图相比,下面的并查集结构要明显好得多!因为我们只需要$\mathcal{O}(1)$的时间就可以轻易查询到任意结点的根结点了。
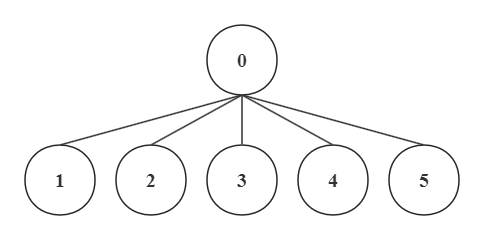
我们把这种形态上的转变称作路径压缩。具体到代码实现方面,只需在查找函数Find(x)中,返回查找到的根结点Find(father[x])之前,将这个结果赋值给当前结点的父结点father[x]即可:
int Find(int x) {
if(x == father[x]) return x;
return father[x] = Find(father[x]);
}因此需要注意:我们是通过查找操作来顺便实现路径压缩的,也就意味着,如果进行了合并操作之后,并没有进行任何的查找操作,也就没有进行任何的路径压缩,此时不能直接通过x == father[x]是否成立来判断x是否属于father[x]为根结点的集合;换言之,father[x]有可能并不是x的真正的根结点!因此,只能通过Find(x)来获取x的根结点。
合并
合并操作也就是将两个不同的集合合并到一起。因此,我们只需将两个集合的“根结点”进行连接(令其中一个结点的父结点是另一个即可)。但是要注意,只能对不同的集合进行合并,如果是同一个集合,不能合并。
void Union(int x, int y) {
int px = Find(x);
int py = Find(y);
if(px != py) father[px] = py;
}寻找并查集中不同集合的个数
注意,在实现并查集算法前,一定要对father数组进行初始化:初始状态每一个结点都是根结点(全部彼此不连通)。
void init(int n) {
int i;
for(i=1; i<=n; i++) father[i] = i;
}完成所有的合并操作后,要求共有几个不同的集合,就直接寻找根结点的个数即可:有几个根,就有几个不同的集合。
int i;
int ans = 0;
for(i=1; i<=n; i++) {
if(father[i] == i) ans++;
}
// ans 即为根结点数量

