研究生的基本素养之线性代数

写在前面

对于包括计算机专业在内的理工科而言，线性代数是一门非常重要的数学基础课。本文立足于申请研究生笔试、面试等等考核，从本科生角度，将《线性代数》这门课中常见的重要知识点做以简单的记录。

正文

行列式与矩阵基础知识

1. 计算3行3列行列式

   $$\left | \begin{array}{c} a_{11} & a_{12} & a_{13} \\ b_{11} & b_{12} & b_{13} \\ c_{11} & c_{12} & c_{13} \end{array} \right | = a_{11}b_{12}c_{13} + a_{12}b_{13}c_{11} + a_{13}b_{11}c_{12} - a_{13}b_{12}c_{11} - a_{11}b_{13}c_{12} - a_{12}b_{11}c_{13}$$

2. 计算矩阵的逆

   请注意，一般来说，只有方阵才可能有逆。对于方阵$A$，我们通常将它和同阶单位阵$I$横向拼接排列写在一起：$A|I$，然后对整体做初等行变换，直至左边的方阵变为单位阵，此时结果为：$I|B$，那么有$A^{-1}=B$。

3. 矩阵可逆的充要条件

   线性代数中，对于方阵$A$，$A$可逆的充要条件包括：

   1. 方阵$A$可逆
   2. 方阵$A$的行列式不为零（非奇异矩阵）
   3. $A$所有的特征值非零
   4. $A$所有的列向量线性无关
   5. $A$满秩
   6. $A$可以表示为若干初等矩阵的乘积

n维向量

线性相关和线性无关的概念一定要明确！

1. 线性相关：对于给定的一组n个向量$\mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_n$，若存在n个不全为零的实数$\lambda_1,\lambda_2,\cdots,\lambda_n$，使得它们与n个向量的线性组合$\displaystyle \sum_{i=1}^N\lambda_i\mathbf{v}_i$等于零，则称这n个向量线性相关；否则称它们线性无关。

2. 向量范数问题：对于给定的n维向量$\mathbf{v}=[v_1,v_2,\cdots, v_n]$

   • 一范数：$\displaystyle ||\mathbf{v}||_1 = \sum_{i=1}^n |v_i|$
   • 二范数：$\displaystyle ||\mathbf{v}||_2 = \sqrt{\sum_{i=1}^nv_i^2} $
   • $\infty$范数：$||\mathbf{v}||_\infty = \max |v_i|$
   • p范数：$\displaystyle ||\mathbf{v}||_p = \left( \sum_{i=1}^nv_i^2 \right)^{\frac{1}{p}}$

3. 标准正交基的概念。

   基指的是满足如下条件的最少向量集合：在向量空间中任取一个其他的向量，它连同该向量集合中的向量都是线性相关的。

   而标准正交基指的就是模长为1，且两两正交的一组基。

线性方程组

1. 对于线性方程组$AX=b$，称n阶方阵$A$为系数矩阵，$[A|b]$为增广矩阵：
   1. 若$r(A)=r(A|b)=n$，则方程组有唯一解；
   2. 若$r(A)=r(A|b)<n$，则方程组有无穷解；
   3. 若$r(A) \ne r(A|b)$，则方程组无解

通过具体的实例体会本章知识点。

例题

解非齐次线性方程组

解下面的非齐次线性方程组。

$$\begin{cases} x_1+5x_2-x_3-x_4=-1 \\ x_1-2x_2+x_3+3x_4=3 \\ 3x_1+8x_2-x_3+x_4=1 \\ x_1-9x_2+3x_3+7x_4=7 \end{cases}$$

第一步，写出线性方程组的增广矩阵。

$$[A|b]=\left [ \begin{array}{c} 1 & 5 & -1 & -1 & -1 \\ 1 & -2 & 1 & 3 & 3 \\ 3 & 8 & -1 & 1 & 1 \\ 1 & -9 & 3 & 7 & 7 \end{array} \right ]$$

第二步，将增广矩阵化简为行阶梯矩阵。

$$\begin{aligned} (A|b) &= \left[ \begin{array}{c} 3 & 8 & -1 & 1 & 1 \\ 1 & 5 & -1 & -1 & -1 \\ 1 & -2 & 1 & 3 & 3 \\ 1 & -9 & 3 & 7 & 7 \end{array}\right] \\ &\to \left[\begin{array}{c} 3 & 8 & -1 & 1 & 1 \\ 1 & 5 & -1 & -1 & -1 \\ 1 & -2 & 1 & 3 & 3 \\ 0 & -7 & 2 & 4 & 4 \end{array}\right] \\ &\to \left[\begin{array}{c} 3 & 8 & -1 & 1 & 1 \\ 1 & 5 & -1 & -1 & -1 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & -7 & 2 & 4 & 4 \end{array}\right] \\ &\to \left[\begin{array}{c} 1 & 5 & -1 & -1 & -1 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & -7 & 2 & 4 & 4 \end{array}\right] \\ &\to \left[\begin{array}{c} 1 & 5 & -1 & -1 & -1 \\ 0 & -7 & 2 & 4 & 4 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]\end{aligned}$$

第三步，判断增广矩阵的秩并求解。

$$r(A|b) = r(A) < 4$$

因此方程组有无穷解。

根据行阶梯矩阵，我们得到

$$\begin{cases} x_1+5x_2-x_3-x_4&=-1 \\ -7x_2+2x_3+4x_4&=4 \end{cases}$$

接下来展示两种求解方法。

第一种，先求齐次方程组通解，再求非齐次方程组特解，组合得到最终解。不妨将$x_3,x_4$看作两个自由元，分别令$x_3=0,x_4=1$以及$x_3=1,x_4=0$，可以得到

$$\xi_1=\left(-\frac{13}{7}, \frac{4}{7}, 0, 1\right)^T, \xi_2=\left( -\frac{3}{7},\frac{2}{7},1,0 \right)^T$$

令自由元$x_3=x_4=0$，得到一个特解

$$\xi_0=\left( \frac{13}{7}, -\frac{4}{7}, 0, 0 \right)^T$$

因此，最终的解形式为

$$\mathbf{x}=\xi_0+k_1\xi_1+k_2\xi_2$$

第二种方法，思考起来、写起来更加简洁，那便是直接用自由元$x_3,x_4$表示出主元$x_1,x_2$：

$$\begin{cases} \displaystyle x_1 = -\frac{3}{7}x_3-\frac{13}{7}x_4+\frac{13}{7} \\ \displaystyle x_2 = \frac{2}{7}x_3+\frac{4}{7}x_4-\frac{4}{7} \end{cases}$$

因此，解可以写成

$$\begin{aligned} \mathbf{x} &= (x_1,x_2,x_3,x_4)^T \\ &=\left(-\frac{3}{7}x_3-\frac{13}{7}x_4+\frac{13}{7}, \frac{2}{7}x_3+\frac{4}{7}x_4-\frac{4}{7}, x_3, x_4\right)^T \\ &= \left( -\frac{3}{7}, \frac{2}{7}, 1, 0 \right)^Tx_3 + \left( -\frac{13}{7}, \frac{4}{7}, 0, 1 \right)^Tx_4 + \left( \frac{13}{7}, -\frac{4}{7}, 0, 0 \right)^T \end{aligned}$$

特征值与特征向量

1. 特征值分解。

   见例题，求特征值与特征向量。

2. 代数重数和几何重数。

   对方阵$A$做特征值分解时，计算出它的全部特征值。

   • 代数重数指的是特征方程根（特征值）的重数；
   • 几何重数指的是单个特征值所对应的线性无关的特征向量的数目。

   几何重数一定不大于代数重数。

3. 矩阵相似

   对于方阵$A$，若存在可逆矩阵$P$，使得$P^{-1}AP=B$，则称$A$与$B$相似，记作$A \sim B$。

4. 矩阵合同

   对于方阵$A$，若存在可逆矩阵$P$，使得$P^TAP=B$，则称$A$与$B$合同，记作$A \simeq B$。

5. 矩阵对角化

   对于方阵$A$，若有$A\sim \Lambda$，其中$\Lambda$为对角矩阵，则称$P^{-1}AP=\Lambda$这个转换过程为矩阵对角化。至于矩阵对角化的过程，详见下面的例题。

6. 施密特正交化

   给定一组向量$\alpha_1, \alpha_2, \cdots, \alpha_n$，要对其进行正交化，就需要用到施密特正交化：

   • $\displaystyle \beta_1=\alpha_1$
   • $\displaystyle \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1, \beta_1)}\beta_1$
   • $\displaystyle \beta_3=\alpha_3 - \frac{(\alpha_3, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_3, \beta_2)}{(\beta_2, \beta_2)}\beta_2$
   • $\dots$
   • $\displaystyle \beta_n = \alpha_n - \frac{(\alpha_n, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\alpha_n, \beta_2)}{(\beta_2, \beta_2)}\beta_2 - \cdots - \frac{(\alpha_n, \beta_{n-1})}{(\beta_{n-1}, \beta_{n-1})}\beta_{n-1}$

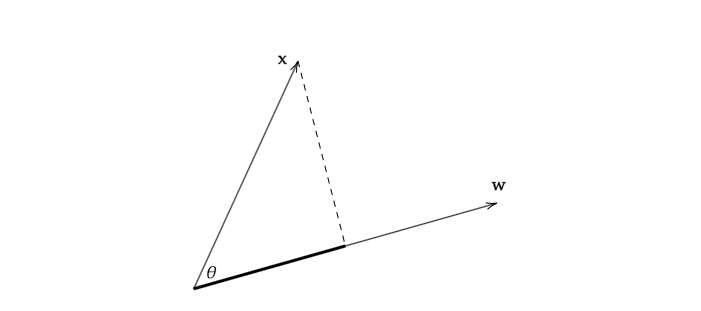
   向量$\mathbf{x}$与$\mathbf{w}$的内积$(\mathbf{x}, \mathbf{w}) = ||\mathbf{x}||_2·||\mathbf{w}||_2·\cos\theta$，而$(\mathbf{x},\mathbf{x})=||\mathbf{x}||_2·||\mathbf{x}||_2$，因此向量$\mathbf{x}$在$\mathbf{w}$上的投影长度为$\displaystyle ||\mathbf{Prj}_{\mathbf{w}}\mathbf{x}||_2 = ||\mathbf{x}||_2·\cos\theta $，而投影则表示为

   $$\mathbf{Prj_{\mathbf{w}}x} = \frac{||\mathbf{x}||_2·\cos\theta}{||\mathbf{w}||_2}\mathbf{w} = \frac{(\mathbf{x}, \mathbf{w})}{(\mathbf{w}, \mathbf{w})}\mathbf{w}$$

   注意，此处的$||\mathbf{x}||_2$表示$\mathbf{x}$的二范数（即模长）。

   因此，$\displaystyle \frac{(\alpha_i, \beta_j)}{(\beta_j, \beta_j)}\beta_j$表示向量$\alpha_i$在$\beta_j$上的投影，进一步地，$\displaystyle \alpha_i - \frac{(\alpha_i, \beta_j)}{(\beta_j, \beta_j)}\beta_j$（比如下图中的虚线部分）则与$\beta_j$正交。

   

7. 奇异值分解。

   对于一般的m×n的矩阵A，无法进行特征值分解，但可以进行奇异值分解：

   $$A = U\Sigma V^T$$
   1. 求$A^TA$的特征值和特征向量，拼接得到矩阵$V$
   2. 求$AA^T$的特征值和特征向量，拼接得到矩阵$U$
   3. $\Sigma$主对角线上的元素称为奇异值$\sigma_i$，$\sigma_i = \sqrt{\lambda_i}$，其中$\lambda_i$为特征值

例题

对角化过程

已知矩阵$A = \left[ \begin{array}{c} 0 & 1 & 1 & -1 \\ 1 & 0 & -1 & 1 \\ 1 & -1 & 0 & 1 \\ -1 & 1 & 1 & 0 \end{array} \right]$，求出正交矩阵$P$与对角矩阵$\Lambda$，使得$A=P^{-1}\Lambda P$。其中

解：

这种题目有一套完整的解题流程，按部就班即可。首先需要求出特征值；然后将特征值代入方程组，利用上一部分的知识点求出方程组的基础解系即为特征向量，然后对于几何重数大于1的特征值对应的特征向量，还需要对其进行施密特正交化；最后得到互相正交的特征向量后，再进行单位化，按列向量进行拼接即可得到正交矩阵$P$。

第一步，求特征值。即解方程组$A\mathbf{x}=\lambda \mathbf{x}$，稍作转化得到

$$(A-\lambda I)\mathbf{x}=0$$

对于该齐次线性方程组，要想存在非零解，则系数矩阵$A-\lambda I$必然不满秩，进而有

$$|A-\lambda I|=0$$

回到本题中，我们写出

$$|A-\lambda I| = \left| \begin{array}{c} -\lambda & 1 & 1 & -1 \\ 1 & -\lambda & -1 & 1 \\ 1 & -1 & -\lambda & 1 \\ -1 & 1 & 1 & -\lambda \end{array} \right| = 0$$

化简得到

$$(\lambda-1)^3(\lambda+3)=0$$

故特征值$\lambda_1=\lambda_2=\lambda_3=1,\lambda_4=-3$。

第二步，求出特征向量。

对于三重根$\lambda_1=\lambda_2=\lambda_3=1$，代入系数矩阵得

$$A-\lambda I = \left[ \begin{array}{c} -1 & 1 & 1 & -1 \\ 1 & -1 & -1 & 1 \\ 1 & -1 & -1 & 1 \\ -1 & 1 & 1 & -1 \end{array} \right]$$

化为行阶梯矩阵为

$$A-I = \left[ \begin{array}{c} 1 & -1 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]$$

得到$x_1-x_2-x_3+x_4$，按照求方程组解的方法可以得到三个基础解系，它们就是$\lambda_1=\lambda_2=\lambda_3=1$对应的特征向量：

$$\begin{cases} \xi_1=(1,1,0,0)^T \\ \xi_2=(1,0,1,0)^T \\ \xi_3=(-1,0,0,1)^T \end{cases}$$

对于一重根$\lambda_4=-3$，代入系数矩阵得到

$$A-\lambda I = \left[ \begin{array}{c} 3 & 1 & 1 & -1 \\ 1 & 3 & -1 & 1 \\ 1 & -1 & 3 & 1 \\ -1 & 1 & 1 & 3 \end{array} \right]$$

化为行阶梯矩阵为

$$A+3I = \left[ \begin{array}{c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right]$$

自由元数量为1，不妨视$x_4$为自由元，得到通解

$$\xi_4=(1, -1, -1, 1)^T$$

第三步，正交化。

不同的特征值对应的特征向量必然正交。而特征值1对应的特征向量有三个，因此只需要对它们三个进行正交化即可。

待正交化的向量组为

$$\begin{cases} \xi_1=(1,1,0,0)^T \\ \xi_2=(1,0,1,0)^T \\ \xi_3=(-1,0,0,1)^T \end{cases}$$

进行施密特正交化：

$$\begin{cases} \displaystyle \beta_1 = \xi_1 = (1,1,0,0)^T \\ \displaystyle \beta_2 = \xi_2 - \frac{(\xi_2, \beta_1)}{(\beta_1,\beta_1)}\beta_1 = \left( \frac{1}{2}, -\frac{1}{2}, 1, 0 \right)^T \\ \displaystyle \beta_3 = \xi_3 - \frac{(\xi_3, \beta_1)}{(\beta_1, \beta_1)}\beta_1 - \frac{(\xi_3, \beta_2)}{\beta_2, \beta_2}\beta_2 = \left( -\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, 1 \right)^T \end{cases}$$

第四步，单位化。

这一步很简单了，只需要对经过施密特正交化处理后的向量归一化为模长为1即可。

$$\begin{cases}\displaystyle \eta_1 = \left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0, 0\right)^T \\ \displaystyle \eta_2 = \left( \frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}, 0 \right)^T \\ \displaystyle \eta_3 = \left( -\frac{1}{\sqrt{12}}, \frac{1}{\sqrt{12}}, \frac{1}{\sqrt{12}}, \frac{3}{\sqrt{12}} \right)^T \end{cases}$$

还需要对$\xi_4=(1, -1, -1, 1)^T$进行单位化：

$$\eta_4 = \left( \frac{1}{2}, -\frac{1}{2}, -\frac{1}{2}, \frac{1}{2} \right)^T$$

第五步，写出最终答案。

求得正交矩阵

$$\begin{aligned} P &= \left[ \begin{array}{c} \eta_1, \eta_2, \eta_3, \eta_4 \end{array} \right] \\ &= \left[ \begin{array}{c} \displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{6}} & \displaystyle -\frac{1}{\sqrt{12}} & \displaystyle \frac{1}{2} \\ \displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{6}} & \displaystyle \frac{1}{\sqrt{12}} & \displaystyle -\frac{1}{2} \\ \displaystyle 0 & \displaystyle \frac{2}{\sqrt{6}} & \displaystyle \frac{1}{\sqrt{12}} & \displaystyle -\frac{1}{2} \\ 0 & 0 & \displaystyle \frac{3}{\sqrt{12}} & \displaystyle \frac{1}{2} \end{array} \right] \end{aligned}$$

求得对角矩阵

$$\begin{aligned} \Lambda &= \mathrm{diag}(\lambda_1, \lambda_2, \lambda_3, \lambda_4) \\ &= \left[ \begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -3 \end{array} \right] \end{aligned}$$

使得$A = P^{-1}\Lambda P = P^T\Lambda P$。

Reference

解线性方程组：https://zhuanlan.zhihu.com/p/144538375

矩阵对角化：https://blog.csdn.net/compression/article/details/49180775

向量内积：https://zhuanlan.zhihu.com/p/157490048

赏