写在前面
对于包括计算机专业在内的理工科而言,概率论与数理统计是一门非常重要的数学基础课。本文立足于申请研究生笔试、面试等等考核,从本科生角度,将《概率论与数理统计》这门课中常见的重要知识点做以简单的记录。
正文
概率论基本知识点
条件概率公式
关于上述第三个公式,有递推公式$P(A_1A_2\dots A_i)=P(A_i|A_1A_2\dots A_{i-1})P(A_1A_2\dots A_{i-1})$,依次递推可得结果。
全概率公式
试验$E$的样本空间有一个划分为$B_1, B_2, \dots, B_n$,则$E$的某一事件$A$的全概率公式为
简单理解,导致事件$A$发生有很多条件因素,用条件概率算加和就是全概率公式。
贝叶斯公式
有时候利用贝叶斯公式计算概率时,分母的$P(B)$需要用全概率公式计算得到。
随机变量及其概率分布
随机变量
随机变量分为两种:
- 离散型随机变量
- 连续型随机变量
分布律与概率密度
- 分布律:针对离散型随机变量的概率分布。即高中学过的分布列。高中主要学习的就是离散型随机变量。
- 概率密度:针对连续型随机变量的概率分布。对连续型随机变量$X$,有概率密度函数$f(x)$,则$P(X=a)=f(a)$。
概率密度函数是重点。它有如下的特点:
- 非负:$\forall x \in (-\infty, +\infty), 0 \leqslant f(x) \leqslant 1$;
- 积分为1:$\displaystyle \int_{-\infty}^{+\infty}f(x)dx=1$
分布函数
对于随机变量$X$,定义它的分布函数
分布函数$F(x)$的性质如下:
- $F(x)$单调不减
- $\displaystyle F(-\infty) = \lim_{x\to -\infty}F(x) = 0; \displaystyle F(+\infty) = \lim_{x\to +\infty}F(x) = 1$
- $F(x)$右连续
几种常见的离散型分布
| 0-1分布 | 二项分布 | 泊松分布 | 超几何分布 | |
|---|---|---|---|---|
| 分布$X$ | $X\sim 0-1(p)$ | $X\sim B(n,p)$ | $X\sim P(\lambda)$ | $X\sim H(N,M,n)$ |
| 分布律$P(X=k)$ | $p^k(1-p)^{n-k}$ | $C_n^kp^k(1-p)^{n-k}$ | $\displaystyle \frac{\lambda^ke^{-\lambda}}{k!}$ | $\displaystyle \frac{C_M^kC_{N-M}^{n-l}}{C_N^n}$ |
| 数学期望$E(X)$ | $p$ | $np$ | $\lambda$ | $\displaystyle n\frac{M}{N}$ |
| 方差$D(X)$ | $p(1-p)$ | $np(1-p)$ | $\lambda$ | $\displaystyle n\frac{M(N-M)(N-n)}{N^2(N-1)}$ |
- 几种常见的连续型分布
| 正态分布 | 指数分布 | 均匀分布 | |
|---|---|---|---|
| 分布$X$ | $X\sim N(\mu,\sigma^2)$ | $X\sim E(\lambda)$ | $X\sim U(a,b)$ |
| 密度函数$f(x)$ | $\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$ | $\lambda e^{-\lambda x}$ | $\displaystyle \frac{1}{b-a}$ |
| 分布函数$F(x)$ | $1-e^{-\lambda x}$ | $\begin{cases} 0,x\leqslant a \\ \displaystyle \frac{x-a}{b-a}, a<x<b \\ 1, x\geqslant b \end{cases}$ | |
| 数学期望$E(X)$ | $\mu$ | $\displaystyle \frac{1}{\lambda}$ | $\displaystyle \frac{a+b}{2}$ |
| 方差$D(X)$ | $\sigma^2$ | $\displaystyle \frac{1}{\lambda^2}$ | $\displaystyle \frac{(b-a)^2}{12}$ |
多元随机变量及其概率分布
多元随机变量相比于单一随机变量,提高了随机变量维度,情况更加复杂。同样地,也有概率密度、分布函数等定义。这里以常见的二元随机变量为例进行说明。
联合分布律与联合概率密度
- 联合分布律:多元随机变量为离散型随机变量
- 联合概率密度:多元随机变量为连续型随机变量。对于连续型随机变量$X,Y$,有概率密度函数$f(x,y)$,则$P(X=a \cap Y=b)=f(a,b)$
分布函数
不妨以连续型随机变量为例,定义$X,Y$的概率分布函数为
边缘分布
即仅保留一个随机变量、消去其他全部变量而得到的概率分布称为边缘分布:
求边缘概率密度时,对于离散型随机变量,边缘概率需要进行求和;对于连续型随机变量,边缘概率密度需要进行积分:
条件概率分布
二维随机变量$X,Y$概率密度为$f(x,y)$,而$(X,Y)$关于$Y$的边缘概率密度为$f_Y(y)$,对于固定的$y$,称$\displaystyle \frac{f(x,y)}{f_Y(y)}$,记作
而称
为$Y=y$条件下$X$的分布函数。
例题
联合概率密度求边缘概率密度
设随机变量$(X,Y)$的联合概率密度函数为
- 求常数$k$;
- 求随机变量$X$的边缘概率密度$f_X(x)$;
- 求$P(Y>X)$。
解析:
求解常数$k$,需要用到性质$\displaystyle \int_0^{+\infty}\int_0^{+\infty}ke^{-(2x+y)}dxdy = 0$,计算得出$k=2$.
根据上面的计算公式
对概率密度进行积分
求条件概率分布
设随机变量$X,Y$的概率分布为
- 求条件概率$P(X<1|Y<1)$;
- 求边缘概率密度$f_X(x)$。
解析:
将概率积分区域表示在平面直角坐标系:
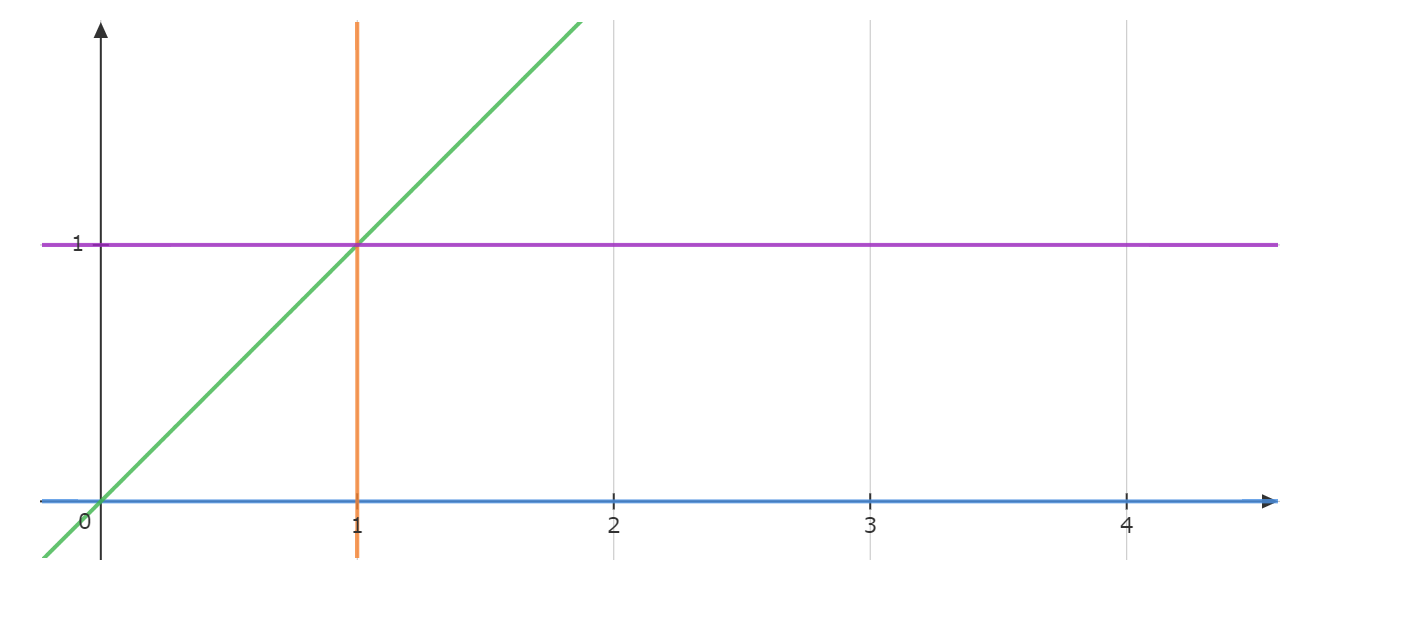
对$x<1,y<1,0<y<x$围成的区域进行积分,不妨将其看作$x$型域:
对$0<y<x,y<1$围成的区域进行积分,不妨将其看作$y$型域:
对$0<y<x$围成的区域进行积分,由于要求$X$的边缘概率,因此将其视为$x$型域:
进行积分:
求两个随机变量的函数的分布
设二维随机变量$(X,Y)$的概率密度为
求$Z=X-Y$的概率密度$f_Z(z)$。
解析:
这种题目通常有两种做法。通常将$Y$(当然$X$也可以)用$Z$和$X$(或者$Y$)的式子表示出来并代入原限制条件,然后将积分区域用$z$型域表出,求积分即可。具体如下。
由$z=x-y$得到$y=x-z$,则
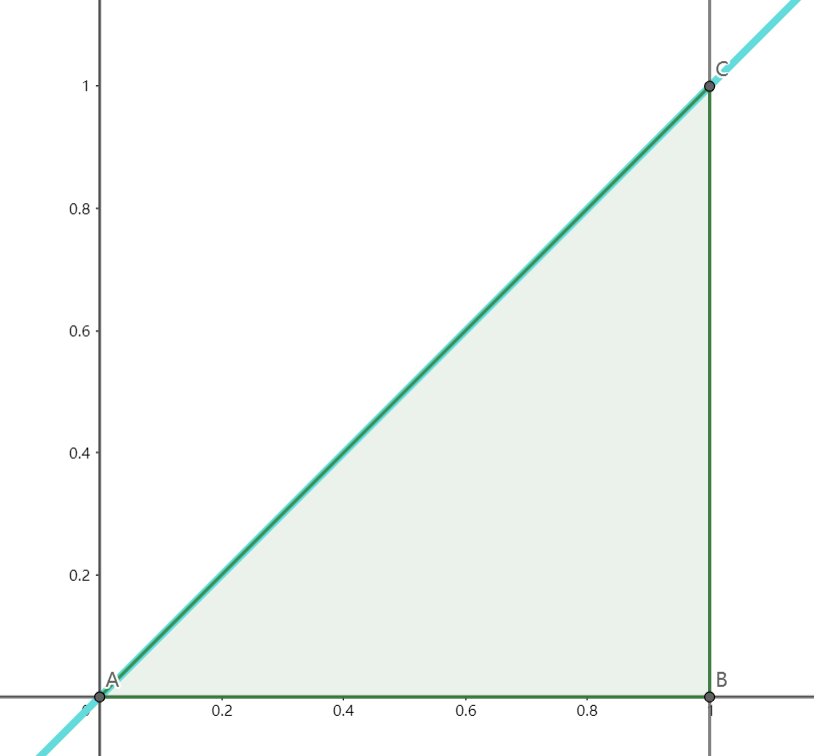
因此,
得到
随机变量的数字特征
期望、方差、矩、协方差和相关系数的计算是笔试中的重点,而大数定律、中心极限定理相关概念知识点经常出现在面试中,请务必掌握。
期望
方差
重要性质:$D(X) = E(X^2) - E^2(X)$
矩
矩:设$X$为随机变量,$c$为常数,$r$为正整数,则$E[(X-c)^2]$称为$X$关于$c$点的$r$阶矩。
原点矩:$c=0$时,$E(X^r)$称为$X$的$r$阶原点矩。
中心距:$c=E(X)$时,$E[(X-E(X))^r]$称为$X$的$r$阶中心距。
协方差
随机变量$X,Y$的协方差定义为
性质:
相关系数
随机变量$X,Y$的相关系数定义为
备注:
- $\rho_{XY}=0$时,说明$X,Y$不(线性)相关,但是它们未必独立,因为这只能说明它们之间不存在线性关系,但是不排除可能存在其他关系
- $|\rho_{XY}|$越靠近1,则说明$X,Y$的线性关系越强烈,取等号时,两者存在严格的线性关系
大数定律
大数定律本质上揭示了“当重复试验次数很大时,随机变量的均值依概率收敛与其期望”,它将数理统计中的均值和概率论中的期望联系在了一起。
三种表述:
辛钦大数定律:随机变量$X_1,X_2,\dots,X_n$相互独立,服从同一分布且具有数学期望$E(X_i)=\mu$,则序列$\displaystyle \bar{X} = \frac{1}{n}\sum_{i=1}^nX_i$依概率收敛于$\mu$;
伯努利大数定律:大量独立重复实验之后,随机事件的频率收敛于概率,即
其中$f_A$指的是$n$次独立重复试验中事件A发生的频数,$p$是事件A发生的概率。
中心极限定理
独立同分布的中心极限定理
设随机变量$X_1,X_2,\dots,X_n$相互独立且服从同一分布、具有期望$E(X_i)=\mu$和方差$D(X_i)=\sigma^2$,当$n$充分大时,近似地有
即均值$\bar{X}$近似服从以$\mu$为均值、$\displaystyle \frac{\sigma^2}{n}$为方差的正态分布。
棣莫弗-拉普拉斯中心极限定理
设随机变量$\eta_n$服从参数为$n,p$的二项分布$B(n,p)$,当$n$充分大时,$\eta_n$近似服从正态分布$N(np,np(1-p))$:
例题
计算期望、方差、协方差
设随机变量$X,Y$的联合概率密度为
求数学期望$E(X),E(Y)$和协方差$Cov(X,Y)$、相关系数$\rho_{XY}$。
解析:
$0\leqslant y < x \leqslant 1$围成的区域即为积分区域,即下图的蓝色区域。将该区域分别表示为$x$型域和$y$型域:
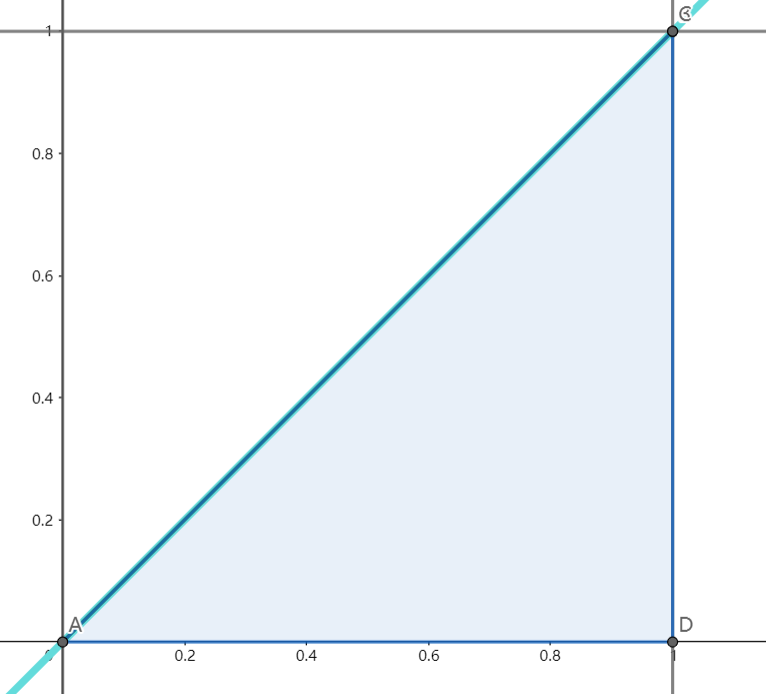
故而有
计算$Cov(X,Y)$还需要计算$E(XY)$,则
故
而计算$\rho_{XY}$还需要计算$D(X),D(Y)$,因此需要用到公式$D(X) = E(X^2) - E^2(X)$.
故
因此得
三大统计分布
卡方分布
设$X_1,X_2,\dots,X_n$是来自标准正态分布$\mathcal{N}(0,1)$的样本,令
则称$X$是自由度为$n$的$\mathcal{X}^2$变量,其分布称为自由度为$n$的$\mathcal{X}^2$分布,记作$X\sim \mathcal{X}^2_n$
上侧$\alpha$分位数:若$X\sim \mathcal{X}^2_n$,记$P(X>\mathcal{X}_\alpha^2(n))=\alpha$,则$c=\mathcal{X}_n^2(\alpha)$称为$\mathcal{X}_n^2$分布的上侧$\alpha$分位数。
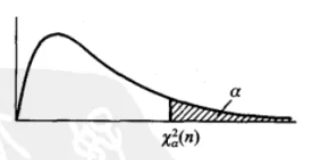
关于上侧$\alpha$分位数的,一定要结合其实际含义进行理解。尤其是$\alpha$的含义,结合概率关系进行理解。注意三大统计分布的图线和x轴围成的区域面积始终为1。
t-分布
设随机变量$X\sim \mathcal{N}(0,1)$,$Y\sim \mathcal{X}_n^2$,且$X,Y$独立,则称
为自由度为$n$的$t$变量,其分布称为自由度为$n$的t-分布,记作$T\sim t(n)$。
上侧$\alpha$分位数:若$T\sim t(n)$,记$P(T>t_{\frac{\alpha}{2}}(n))=\frac{\alpha}{2}$。根据t-分布图像对称性,有重要性质

F-分布
设随机变量$U\sim \mathcal{X}^2(n_1), V\sim \mathcal{X}^2(n_2)$,且它们互相独立,则称随机变量
为服从自由度为$(n_1,n_2)$的F分布,记作$F\sim F(n_1,n_2)$。
上侧$\alpha$分位数:若$F\sim F(n_1,n_2)$,记$\displaystyle P(F>F_{\frac{\alpha}{2}}(n_1,n_2))=\frac{\alpha}{2}$。有重要性质:
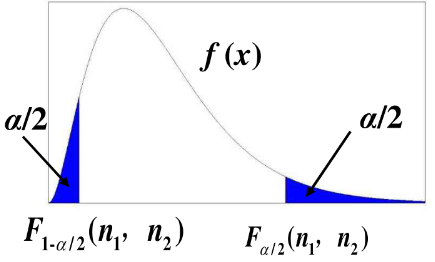
正态分布总体的样本均值与样本方差的分布
设$X_1,X_2,\dots,X_n$是来自正态分布$\mathcal{N}(\mu,\sigma^2)$的样本,样本均值为$\bar{X}$,样本方差为$S^2$,则有几条重要定理,需要掌握:
样本均值$\bar{X}$满足
也即
样本均值$\bar{X}$与样本方差$S^2$相互独立,且
有统计量满足t分布
上面的三个统计量以及其满足的分布非常重要,在后续的假设检验部分有着非常关键的应用。
参数估计
矩估计、极大似然估计都是必须掌握的重要知识点。
矩估计
我们回到矩的定义:
- $k$阶原点矩:设$X$为随机变量,$E(X^k)$称为$X$的$k$阶原点矩,简称$k$阶矩。
- 样本$k$阶矩:称$\displaystyle A_k=\frac{1}{n}\sum_{i=1}^nX_i^k$为样本$k$阶矩。
矩估计的基本原理:样本$k$阶矩$A_k$是$k$阶总体矩$\mu_k=E(X^k)$的无偏估计。也就是在解题过程中,利用恒等式
进行求解参数。通常我们最多使用到两个等式$A_1=E(X),A_2=E(X^2)$:
- 求$E(X)$,$\displaystyle E(X) = \int_{-\infty}^{+\infty}f(x)dx$
- 求$E^2(X)$,$E(X^2) = D(X) + E^2(X)$
极大似然估计
不妨就以连续型随机变量为例。设$X_1,X_2,\dots,X_n$是来自总体$X$的$n$个随机样本,而$x_1,x_2,\dots,x_n$是对应于$X_1,X_2,\dots,X_n$的样本值,则事件$\{X_1=x_1,X_2=x_2,\dots,X_n=x_n\}$发生的概率为
我们需要求出使得$L(\theta)$最大的参数值$\hat{\theta}$。如果将$\theta$的取值范围记作$\Theta$,则
这实际上就是一个简单的优化问题。只需求导数,令其等于0,即可求出最优参数值(也称极大似然估计值)。
为了简化运算,我们往往对$L(\theta)$取对数,得到对数似然函数$\ln L(\theta)$,再对其求导数,令其等于0,同样可以求出最优参数值。
区间估计
我们简单看看区间估计的原理。对于给定值$\alpha$和来自总体$X$的样本$X_1,X_2,\dots,X_n$,我们需要找到两个统计量$\underline{\theta}(X_1,X_2,\dots,X_n) <\theta < \overline{\theta}(X_1,X_2,\dots,X_n)$,满足
则称区间$(\underline{\theta}, \overline{\theta})$是$\theta$的置信水平(置信度)为$1-\alpha$的置信区间。
对于给定的连续型随机变量,我们通常按照$P\{\underline{\theta} < \theta < \overline{\theta}\} = 1-\alpha$来求出置信区间;对于离散型随机变量,通常只能尽可能地选取置信区间使$P\{\underline{\theta} < \theta < \overline{\theta}\} = 1-\alpha$逼近$1-\alpha$。
要想掌握好这一部分的内容,需要更好地回顾、掌握之前的两个部分的知识:
- 三个统计发布中的三个重要定理
- 上$\alpha$分位数的概念
另外我们只关注单个总体$\mathcal{N}(\mu,\sigma^2)的情况$。
$\sigma^2$已知,$\mu$未知时$\mu$的区间估计
设总体$X \sim \mathcal{N}(\mu,\sigma^2)$,$\sigma^2$已知、$\mu$未知,设$X_1,X_2,\dots,X_n$是来自$X$的样本,求$\mu$的置信水平为$1-\alpha$的置信区间。
我们需要找到一个除了未知参数$\mu$之外不依赖于任何未知参数的统计量。这时就需要用到三大统计分布的重要定理(正态分布总体的样本均值与样本方差的分布)。我们选取
我们把统计量$\displaystyle \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$称为枢轴量。
然后,根据标准正态分布的上$\alpha$分位数的定义,可以得到
对左侧括号中的不等式做变形,可以得到
因此求得$\mu$的置信区间为
$\sigma^2$未知,$\mu$未知时$\mu$的区间估计
这种情况下,就不可以使用枢轴量$\displaystyle \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$了,因为$\sigma$是未知的。但是,考虑到$S^2$是$\sigma^2$的无偏估计,因此选用枢轴量$\displaystyle \frac{\bar{X}-\mu}{S/\sqrt{n}}$:

因此有
根据上图所示的上$\alpha$分位数,单个黑色区域面积为$\displaystyle \frac{\alpha}{2}$,全部的黑色区域面积加起来就是$\alpha$,白色区域面积为$1-\alpha$,刚好就是上式的通俗描述。其他的区间估计都可以以此类似理解。
整理得到$\mu$的一个置信水平为$1-\alpha$的置信区间
$\sigma^2$未知,$\mu$未知时$\sigma^2$的区间估计
这时要选去的枢轴量为
因此有
整理得到$\sigma^2$的一个置信水平为$1-\alpha$的置信区间
例题
点估计
设总体$X$的概率密度函数为
其中$\theta>-1$,若$X_1,X_2,\dots,X_n$为来自总体$X$的样本,求参数$\theta$的矩估计和极大似然估计。
解析:
对于矩估计,求出
由$A_1=E(X)$,得
对于极大似然估计,
因此,当$0<x_{(1)}<x_{(n)}<1$时,对数似然函数为
令
得
区间估计
设一次考试的成绩服从正态分布$\mathcal{N}(\mu,\sigma^2)$,其中$\mu,\sigma^2$均未知,现从中随机抽取256个考生的成绩,测得样本均值$\bar{x}=60$,样本标准差$s=16$,求$\mu$的置信度为0.90的置信区间。
解析:
由于需要求出$\mu,\sigma^2$均未知时$\mu$的置信区间,因此选取枢轴量为
由置信水平$1-\alpha=0.9$得$\alpha=0.1$,同时根据上侧$\alpha$分位数,得
将左侧不等式进行整理,即可得到
置信区间为
代入$\bar{x}=60,s=16,n=256,\alpha=0.1$得到最终结果
区间估计是后面假设检验的重要前导知识,必须掌握。
假设检验
先来看一种假设检验问题的基本表述:
在显著性水平$\alpha$下,检验假设
也即“在显著性水平$\alpha$下,针对$H_1$检验$H_0$”。其中,$H_0$称为原假设,$H_1$称为备择假设。和区间估计中类似地,我们也需要选取一个统计量来帮助我们对假设进行检验,这样的统计量被称为检验统计量。而检验统计量的一旦落入某个区域$C$时,就可以拒绝原假设$H_0$,这样的区域$C$称为拒绝域。
另外,注意到,备择假设中的$\mu>0,\mu<0$均可能成立,因此上面这种形式的假设检验被称为双边假设检验。我们选取的检验统计量为
显著性水平为$\alpha$时,拒绝域为
当然,与之相对地,还有左边检验和右边检验,分别为
和
与区间估计类似
- 检验$\mu$,若$\sigma^2$已知,进行Z检验,选取检验统计量$\displaystyle Z=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \stackrel{H_0为真}\sim \mathcal{N}(0,1)$
- 检验$\mu$,若$\sigma^2$未知,进行t检验,选取检验统计量$\displaystyle t=\frac{\bar{X}-\mu_0}{S/\sqrt{n}} \stackrel{H_0为真} \sim t(n-1)$
- 检验$\sigma^2$,若$\mu$未知,进行$\mathcal{X}$检验,选取检验统计量$\displaystyle \mathcal{X}^2=\frac{(n-1)S^2}{\sigma_0^2} \stackrel{H_0为真}\sim \mathcal{X}^2(n-1)$
常见的假设检验置信区间以及单侧置信上下限如下图。




